Gruppo di simmetrie

 

 

Simmetria di un sistema S: ogni trasformazione isometrica o, piu' concisamente, ogni isometria che trasformi S in se stesso.

Operazione di simmetria: ogni trasformazione o, piu' concisamente, ogni movimento attraverso il quale i punti di un sistema S, vanno a corrispondere con ben determinati punti di S stesso.

Gruppo di simmetrie. L'insieme di tutte le operazioni di simmetria di un sistema S, forma gruppo in senso matematico In tal caso si parla di gruppo di simmetrie. Per indicarlo si puo'usare una lettera, ad es G.

 

Gruppo di simmetria del rettangolo

Corrispondenze tra vertici (leggere riga per colonna)

 

rifl1

rifl2

180°

rifl1

A

C

D

rifl2

C

A

B

180°

D

B

A

 


 

Definizione e Prime Proprietà

 

 

 

Definizione 1   Una coppia $(G,*)$, dove $G$è un insieme non vuoto e $*$è una operazione binaria su $G$

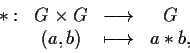
\begin{displaymath}\begin{array}{cccc} *: & G\times G &\longrightarrow & G \\ \quad &(a,b) & \longmapsto & a*b , \end{array}\end{displaymath}


è detta gruppo se valgono le seguenti proprietà:

1)

$*$è associativa:
$\forall a,b,c \in G$si ha $a*(b*c) = (a*b)*c$.

2)

Esiste $e$in $G$tale che $e*a = a*e = a$;
$e$è detto elemento neutro di $G$.

3)

Per ogni $a$appartenente a $G$, esiste $a'$in $G$tale che $a*a'=a'*a = e$;
$a'$è detto inverso di $a$in $G$.

Se l'operazione $*$è anche commutativa, cioè $a*b = b*a$, $\forall a,b\in G$, $(G,*)$è detto gruppo abeliano o commutativo.




 

Osservazione 2   Se $(G,*)$è un gruppo, allora:

1)

l'elemento neutro è unico.
Infatti se $e$e $e'$sono elementi neutri, si ha :
$e = e*e' = e'$.

2)

$\forall a \in G$, esiste un unico inverso $a'$.
Infatti se $a'$e $a''$sono inversi di $a$, si ha:
$a' = a'*e = a'*(a*a'') = (a'*a)*a'' = e*a''= a''$.

Notazione 3   L'operazione $*$definita nell'insieme $G$si indica quasi sempre con $+$o con $\cdot $.
Nel primo caso si parla di gruppo additivo, l'elemento neutro viene indicato con $0$e per ogni $a\in G$, l'inverso $a'$viene chiamato opposto ed è indicato con $-a$.
Nel secondo caso invece si parla di gruppo moltiplicativo, l'elemento neutro viene denotato con $1$e per ogni $a\in G$l'inverso di $a$è indicato con $a^{-1}$.
Scriveremo più brevemente ``gruppo $G$'' invece di ``gruppo $(G,*)$''.
La notazione usata quasi sempre sarà quella moltiplicativa.
Indicheremo inoltre il prodotto di due elementi $a,b$di $G$, con $a\cdot b$o $ab$.

Esempi 4  

1)

$(\mathbb{N} ,+)$, $(\mathbb{N} ,\cdot )$non sono gruppi: non per tutti gli $n\in\mathbb{N} $esiste l'inverso.

2)

$(\mathbb{Z} ,+) $è un gruppo il cui elemento neutro è lo $0$.
$(\mathbb{Z} ,\cdot)$non è invece un gruppo.

 


Sottogruppi

 

Definizione 1   Sia $G$un gruppo e sia $H$un suo sottoinsieme; $H$è un sottogruppo di $G$se sono verificate le seguenti condizioni:

1)

$1\in H$;

2)

$\forall h_{1}, h_{2}$ $\in H$, $h_{1}h_{2}$ $\in H$;

3)

$\forall h\in H$, $h^{-1}\in H$.

Osservazione 2   Se $H$è un sottoinsieme non vuoto di un gruppo $G$, la condizione $1$della definizione 1 può essere dedotta dalle condizioni $2$e $3$: se $a\in H$, $1=a a^{-1}\in H$.
La condizione $2$della definizione 1 si esprime dicendo che $H$è chiuso rispetto al prodotto.

 

Osservazione 3   Sia $H$un sottoinsieme non vuoto di $G$; $H$è un sottogruppo di $G$se e solo se $h_{1} h_{2}^{-1}\in H$, $\forall h_{1},h_{2}\in H$.
Infatti se $H$è un sottogruppo di $G$, ovviamente $h_{1} h_{2}^{-1}\in H$, $\forall h_{1},h_{2}\in H$; viceversa se $\forall h_{1},h_{2}\in H$, $h_{1} h_{2}^{-1}\in H$, si ha:

Proposizione 4   Sia $G$un gruppo. Allora:

1)

se $H$è un sottogruppo di $G$, $H$con l'operazione $\cdot$ristretta ad $H$stesso, è un gruppo;

2)

se $\{\,H_{i}\,\}_{i\in I}$è una famiglia di sottogruppi di $G$, anche $H$= $\bigcap_{i\in I}H_{i}$è un sottogruppo di $G$.

Dimostrazione
La prima affermazione è ovvia; per provare la seconda osserviamo che:


SIMMETRIA (file pdf)