[L12s] Ottica geometrica - (versione sintetica) [Nota]
FG2Bio16/L12s | Docente: F. Bloisi; CdL: Biomedica; a.a.: 2016/2017; studenti: A-O
Indice
Last updated Mon 6 Feb 2017 13:05:23 CET1. Generalità
1.1. Cosa è l'ottica geometrica?
L'ottica geometrica è essenzialmente un insieme di costruzioni geometriche che consentono di seguire il percorso dei raggi luminosi ed è utilizzata per descrivere il comportamento in tutte le situazioni in cui non intervengono fenomeni che ne evidenziano la natura ondulatoria (ad es. interferenza, difrazione, etc.) o corpuscolare (ad es. effetto fotoelettrico, fluorescenza, etc.).
1.2. A che serve l'ottica geometrica?
La progettazione di una semplice lente da occhiali o di un complesso obiettivo "zoom" di una macchina fotografica utilizzano in gran parte l'ottica geometrica anche se alcuni "dettagli" (per ottenere ed es. un effetto fotocromico o antiriflesso) richiedono una trattazione che tenga conto della natura ondulatoria o corpuscolare della luce.
Nella moderna "computer graphics" il "rendering" fà largo uso del "raytracing", tecnica che consiste nel seguire a ritroso, utilizzando le regole dell'ottica geometrica, il percorso dei raggi luminosi che ragguingono ciascun "pixel" del sensore dell'ipotetica macchina fotografica che stà riprendendo la scena. L'immagine di copertina di questa lezione è un bell'esempio di immagine "totalmente artificiale" ottenuta tramite un programma di raytracing (per maggiori dettagli seguire il link sull'immagine).
1.3. Quale è lo scopo di questa lezione?
Questa lezione si limita a presentare in maniera molto sintetica le basi dell'ottica geometrca. Dopo aver definito il concetto di "raggio luminoso", enunceremo le leggi dell'ottica geometrica e ci limiteremo ad applicarle ad un caso, il diottro sferico, molto semplice ma ben rappresentativo di situazioni più complese che si incontrano nello studio dei sistemi ottici.
1.4. Cosa fare per approfondire l'argomento?
Per lo studente che abbia interesse o necessità di approfondire argomenti relativi all'ottica geometrica un buon punto di partenza è dato dal Modulo Basic Geometrical Optics del corso "Fundamentals of Photonics" liberamente accessibile sul sito SPIE (The International Society for Optics and Photonics).
2. Il concetto di "raggio luminoso"
In ottica geometrica è essenziale il concetto di raggio luminoso che può avere varie interpretazioni (traiettorie dei fotoni, curve ortogonali ai fronti d'onda o alle supefici a fase costante, linee di campo del vettore di Poynting, curve tangenti ai vettori d'onda in un'onda piana, etc.), ma di cui è opportuno dare qui una definizione operativa, al fine di rendere l'ottica geometrica indipendente dall'interpretazione, ondulatoria (onde elettronagnetiche) o corpuscolare (fotoni), che si voglia dare della luce.
Nella pratica accade di dover associare al raggio luminoso grandezze fisiche che, in ottica geometrica, possono essere definite solo in maniera empirica: la lunghezza d'onda (percepita dall'occhio come un "colore puro", ad esempio quelli visibili in un arcobaleno, selezionabile tramite un prisma), la polarizzazione (selezionabile tramite un cristallo birifrangente), l'intensità luminosa (valutabile per confronto con una sorgente campione).
Operativamente, un raggio luminoso è costituito dalla luce che si propaga al di là di uno schermo opaco su cui è stato praticato un foro di dimensioni piccole rispetto alle dimensioni dei componenti ottici, ma abbastanza grandi da non dar luogo a fenomeni di diffrazione. In altre parole il foro deve essere grande rispetto alla lunghezza d'onda della luce visibile che sappiamo essere dell'ordine di mezzo millesimo di millimetro (pari a \( 500 \ \text{nm} \)).
Altra grandezza essenziale in ottica geometrica è l'indice di rifrazione (legato, alla velocità di propagazione delle onde elettromagnetiche) che in ottica geometrica viene definito, come vedremo più avanti, tramite la legge della rifrazione.
Sebbene non sia indispensabile fare un collegamento tra raggi luminosi ed onde elettromagnetiche può essere di aiuto tener presente che un fascio di raggi luminosi tra loro paralleli rappresenta un'onda piana, mentre un fascio di raggi luminosi divergenti da (convergenti verso) un punto rappresenta un'onda sferica progressiva (regressiva).

3. Le leggi dell'ottica geometrica
Il comportamento di un qualunque sistema ottico può essere studiato seguendo il percorso dei raggi luminosi che lo attraversano e per far ciò è sufficiente utilizzare le leggi dell'ottica geometrica.
Sperimentalmente si osserva che
Se un raggio luminoso (raggio incidente) raggiunge la superficie di separazone tra due mezzi trasparenti aventi carateristiche ottiche differenti si generano, in genere, due ulteriori raggi luminosi: uno (raggio riflesso) che si propaga nel mezzo da cui provenva il raggio incidente, ed un'altro (raggio rifratto) che si propaga nell'altro mezzo. Il piano che contiene il raggio incidente e la normale alla superficie di separazione si chiama piano di incidenza e l'angolo \( \vartheta_1 \) tra raggio incidente e normale è detto angolo di incidenza.
Sperimentalmente si osserva che
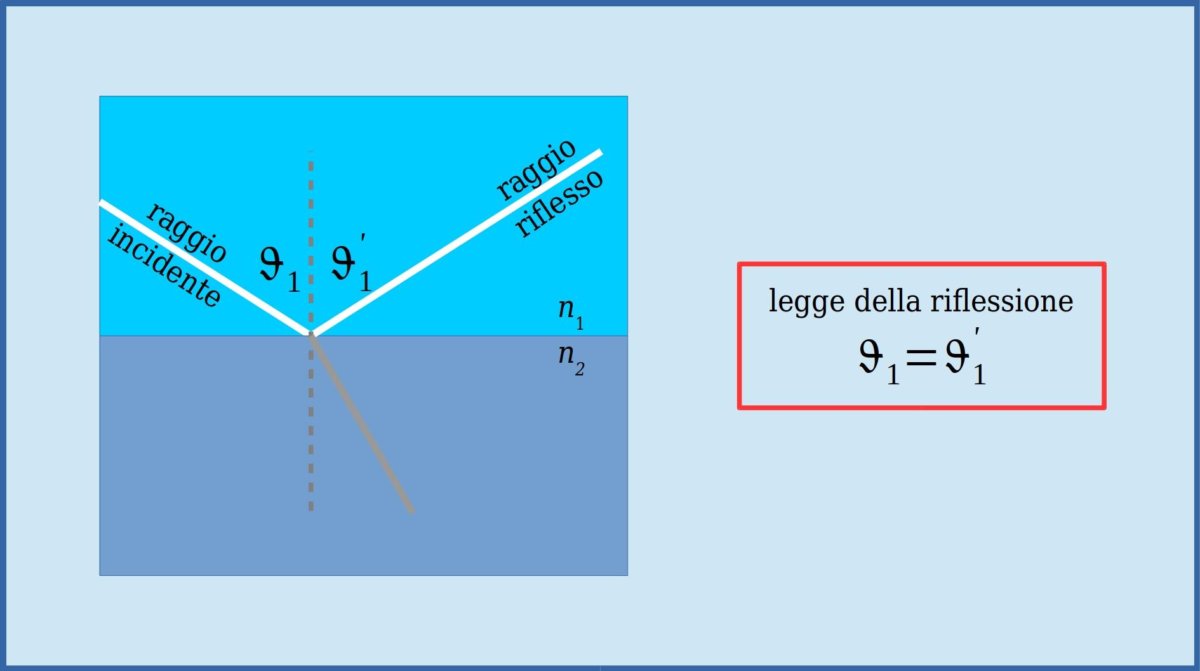
Le costanti \( n_1 \) ed \( n_2 \), che dipendono dalle caratteristiche ottiche dei due mezzi trasparenti, sono dette indice di rifrazione del mezzo 1 e del mezzo 2, rispettivamente. Nell'ambito dell'ottica geometrica l'indice di rifrazione deve essre determinato sperimentalmente assumendo che il vuoto (con buona approssimazione anche l'aria) abbia indice di rifrazione unitario. Eccetto che per il vuoto, l'indice di rifrazione è sempre maggiore dell'unità e dipende dal "colore" (lunghezza d'onda) della luce. Ciò vuol dire che se il raggio incidente non è monocrmatico non si ha un singolo raggio rifratto ma un fascetto "iridescente" di raggi rifratti.
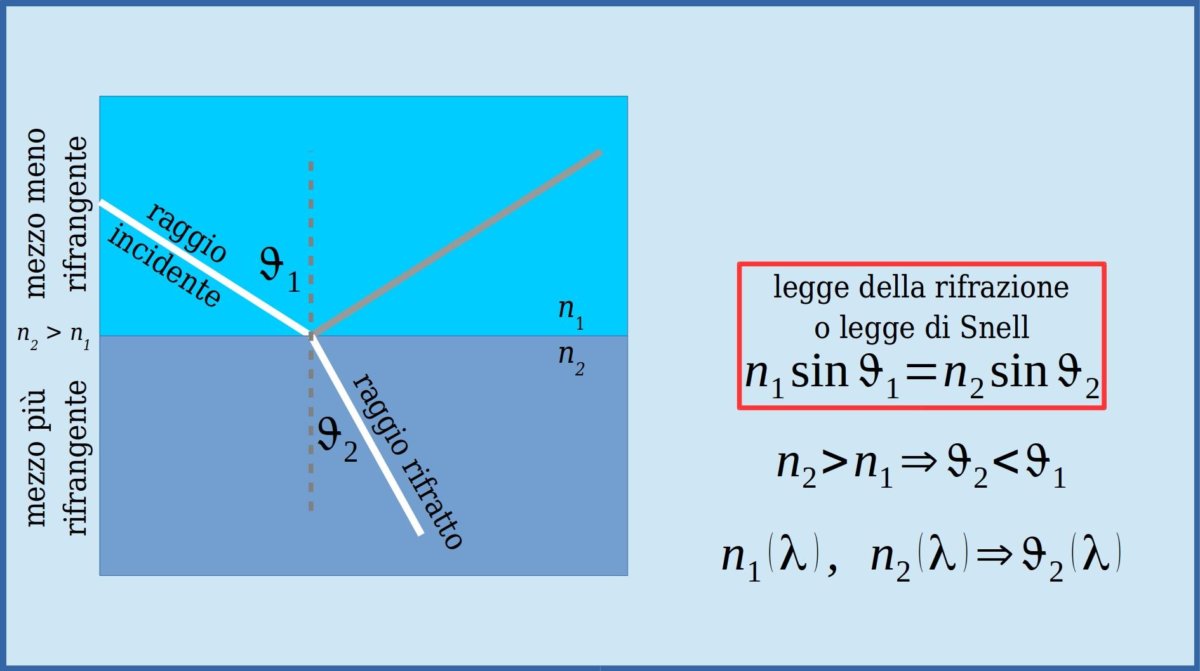
L'intensità del raggio riflesso e di quello rifratto dipendono dalle caratteristiche ottiche dei due mezzi ed anche dall'angolo di incidenza, ma l'ottica geometrica non è in grado di darne una spiegazione. In alcune applicazioni è utile fare in modo che sia predominante la riflessione (in tal caso si parla di specchi), mentre in altre è utile fare in modo che predomini la rifrazione (in tal caso si parla di diottri).
3. Studio di un sistema ottico elementare: il diottro sferico
La maggior parte dei sistemi ottici (da una semplice lente a contatto ad un complesso "zoom" di una macchina fotografica) sono costituiti da un insieme di diottri, concavi o convessi, sferici o meno. Questi, insieme agli specchi, costituiscono i sistemi ottici elementari, che possono essere interpretati come gli elementi di base utilizzati per progettare e costruire i sistema ottico composito.
Prima di procdere è necessario stabilire alcune convenzioni.
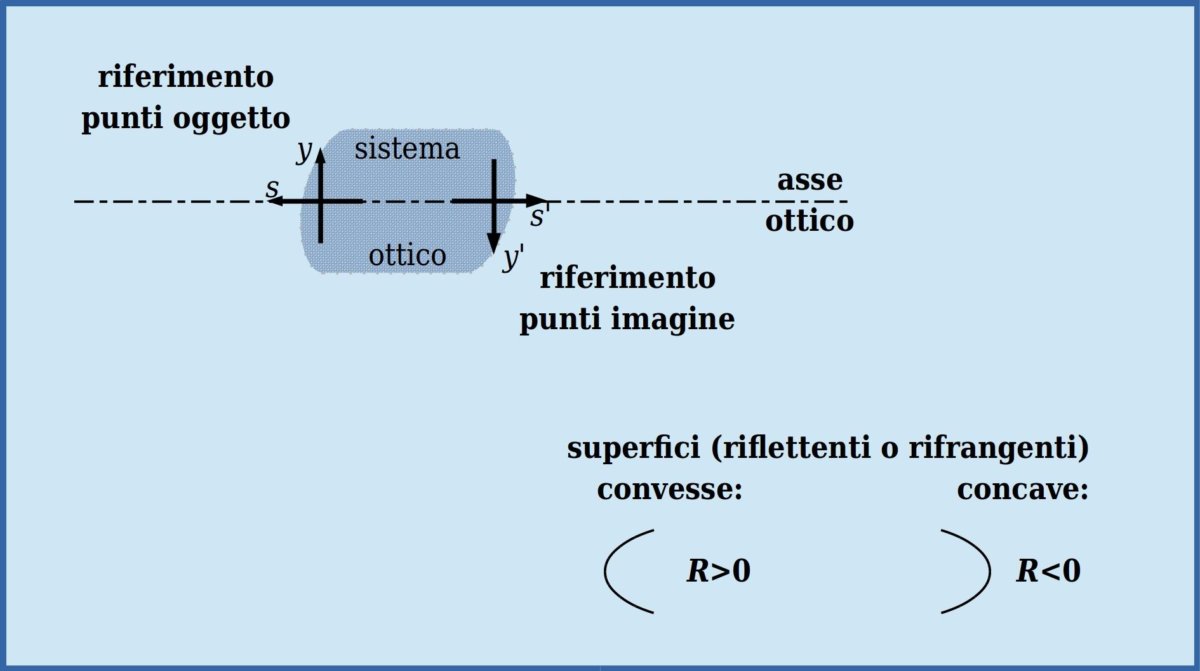
In un sistema ottico si utilizzano due differenti sistemi di riferimento, uno \( x, y, s \) per le sorgenti ed un'altro \( x', y', s' \) per le immagini. Un punto sorgente è un punto da cui provengono (sorgente reale) o da cui sembrano provenire (sorgente virtuale) i raggi luminosi che raggiungono il sistema ottico. Un punto immagine è un punto verso cui convergono (immagine reale) o verso cui sembrano convergere, (imagine virtuale) i raggi luminosi dopo aver attraversato il sistema ottico.
Inoltre i raggi di curvatura delle superfici sono considerati positivi per le superfici convesse e negativi per le superfici concave.
A titolo di esempio presentiamo qui la costruzione geometrica che, tenendo conto della legge di Snell, consente di seguire il percorso di un raggio luminoso che attraversa un diottro sferico convesso. Ci limitiamo all'approssimazione di raggi parassiali, ossia quelli che formano, rispetto all'asse ottico, angoli (\( \alpha \) ed \( \alpha' \) nella figura) piccoli, tali che si possa assumere \( \text{sin} \ \alpha \simeq \alpha \) e \( \text{tan} \ \alpha \simeq \alpha \), se gli angoli sono misurati in radianti.
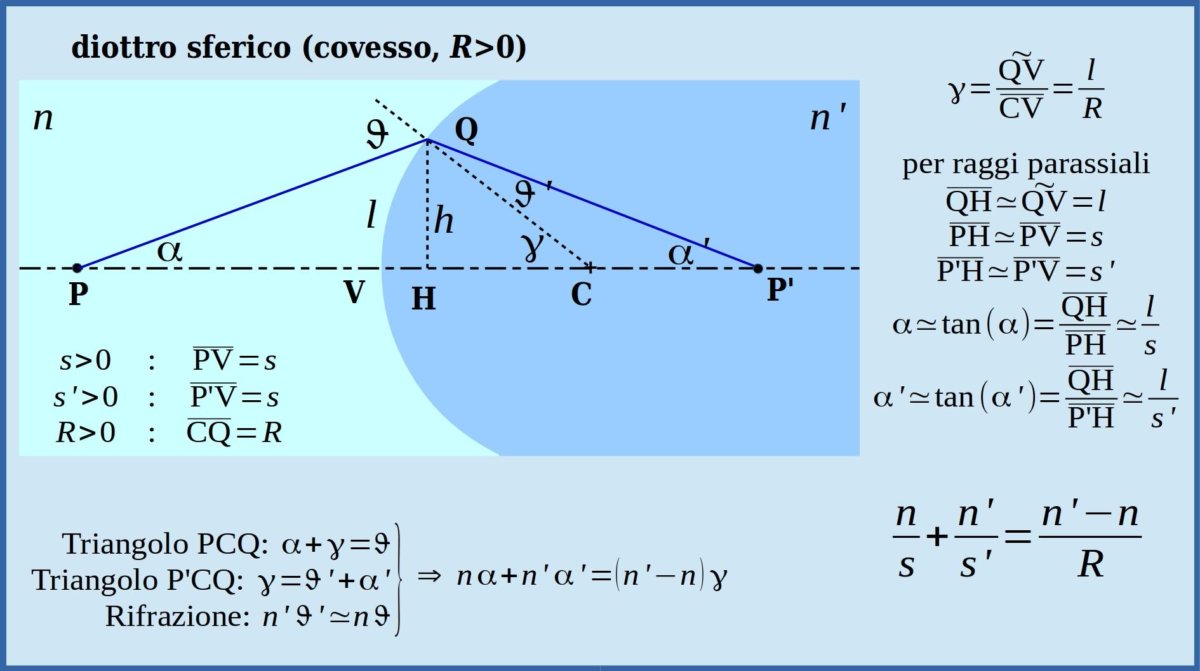
La relazione tra la posizione di un punto sorgente e quella del corrispondente punto immagine (detti punti coniugati, \( \text{P} \) e \( \text{P}' \) nella figura) posti sull'asse ottico del diottro è
Partendo dal punto sorgente \( \text{P} \) posto sull'asse del sistema ottico, tracciamo un raggio parassiale fino ad incontrare il diottro in \( \text{Q} \). Un raggio parassiale deve essere tale che sia \( \text{sin} \ \alpha \simeq \alpha \). Se ci limitiamo ad utilizzare 3 cifre significative troviamo che ciò vale per angoli fino a circa \( 0.144\ \text{rad} = 8.25^{\text{o}} \), tuttavia nella figura, per rendere più chiare le costruzioni geometriche, è stato utilizzato un angolo nettamente maggiore.
Dal punto \( \text{Q} \) tracciamo la normale alla superficie rifrangente. Poichè il diottro è costituito da una superficie sferica il cui centro è in \( \text{C} \), la normale si sovrappone al raggio \( \text{CQ} \). L'angolo \( \vartheta \) tra raggio incidente e normale è l'angolo di incidenza.
Applicando la legge di Snell possiamo determinare l'angolo di rifrazione \( \vartheta' \) e tracciare il raggio rifratto \( \text{QP}' \) fino ad intersecare l'asse del sistema nel punto immagine \( \text{P}' \).
Se l'angolo \( \alpha \) è piccolo (raggi parassiali) anche gli angoli \( \vartheta \) e \( \vartheta' \) sono piccoli per cui possiamo scrivere la legge di Snell come \[ n \ \vartheta \simeq n' \ \vartheta' \]
Nel triangolo \( \text{PCQ} \), l'angolo esterno in \( \text{Q} \), \( \vartheta \), è pari alla somma dei due angoli interni non adiacenti, in \( \text{P} \), \( \alpha \), ed in \( \text{C} \), \( \gamma \): \[ \vartheta = \alpha + \gamma \] Nel triangolo \( \text{P}'\text{CQ} \), con considerazioni analoghe, si trova \[ \gamma = \vartheta' + \alpha' \] e, da queste tre relazioni si ricava facilmente \[ n \alpha + n' \alpha' = \left( n' - n \right) \gamma ~~~\text{(*)} \]
Poiché vogliamo individuare la posizione del punto sorgente \( \text{P} \) tramite la sua distanza \( s = \overline{\text{PV}} \) dal vertice \( \text{V} \) del diottro dal triangolo \(\text{PHQ}\), retto in \(\text{H}\) ricaviamo \[ \text{tan} \ \alpha = \frac{\overline{\text{QH}}}{\overline{\text{PH}}} \] e, se l'angolo \( \alpha \) è piccolo (raggi parassiali) per cui \( \text{tan}\ \alpha \simeq \alpha \), \( \overline{\text{QH}} = h \simeq l \) e \( \overline{\text{PH}} \simeq \overline{\text{PV}} = s \), possiamo scrivere \[ \alpha \simeq \frac{l}{s} \]
Con considerazioni analoghe relative al triangolo \(\text{P}'\text{HQ}\), ricaviamo \[ \alpha' \simeq \frac{l}{s'} \] mentre dalla definizione di angolo in radianti otteniamo \[ \gamma = \frac{l}{R} \]
Sostituendo le espressioni di \( \alpha \), \( \alpha' \) e di \( \gamma \) appena trovate nell'equazione (*) otteniamo l'equazione del diottro.
In effetti la relazione trovata per un diottro convesso (\( R \gt 0 \)) vale anche per un diottro concavo, ponendo \( R \lt 0 \), per un diottro piano, ponendo \( R \to \infty \), e addirittura per uno specchio (concavo, convesso o piano a seconda del valore di \( R \)), ponendo \( n' = -n \).
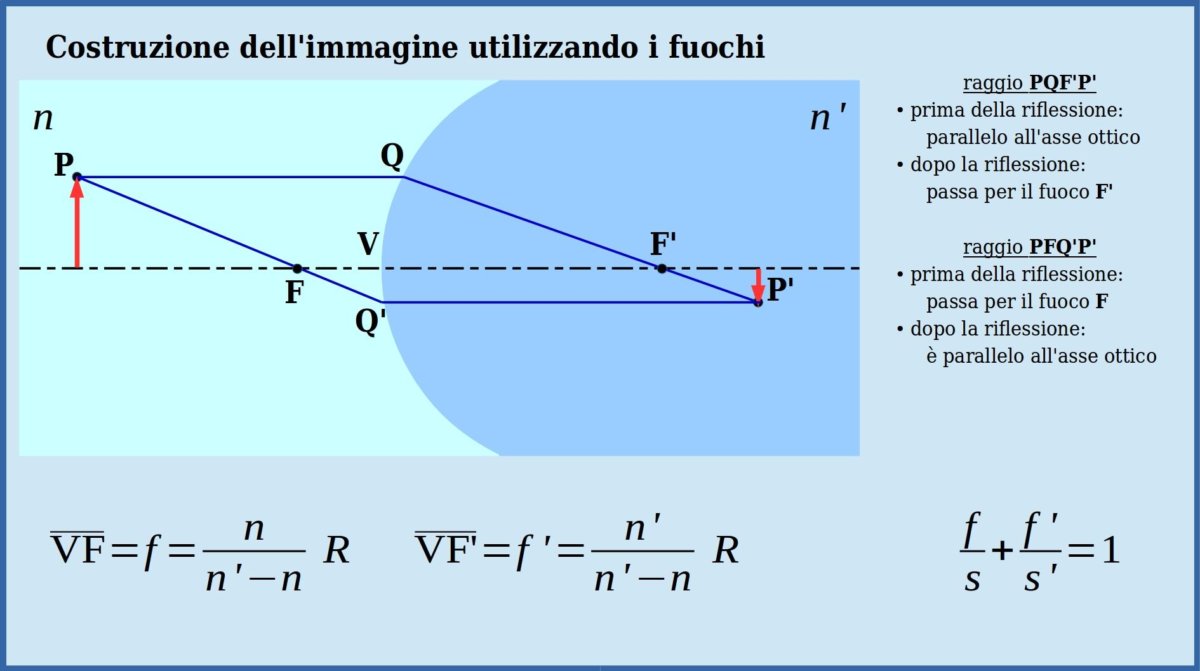
I punti coniugati dei punti all'infinito sono detti fuochi e ponendo rispettivamente \( s \to \infty \) oppure \( s' \to \infty \) si determinano le lunghezze focali
Poiché la posizione dei fuochi, e quindi le lunghezze focali, possono essere anche determinate sperimentalmente, è comodo scrivere la relazione tra punti coniugati facendo compairire solo le lunghezze focali (\( f \), \( f' \)) e non i dettagli costruttivi (\( n \), \( n' \), \( R \)) del diottro:
Anche questa relazione, trovata in un caso particolare, ha validità molto più generale ma, in questa sede, non approfondiremo ulteriormente l'argomento.
I fuochi possono essere utilizzati, con una semplice costruzione geometrica, per determinare la posizione di punti coniugati non sull'asse ottico del diottro.