UNIVERSITA’ DEGLI STUDI DI NAPOLI
“FEDERICO
II”
FACOLTA’ DI INGEGNERIA
CORSO DI LAUREA IN INGEGNERIA MECCANICA
Dipartimento di Ingegneria Meccanica per l’Energetica
Tesi di laurea in
Meccanica delle vibrazioni
INFLUENZA DELLA FLESSIBILITA’ STRUTTURALE
DELL’AVANTRENO SULLA DINAMICA DEL MOTOCICLO
SOMMARIO
Relatore Candidati
Ch.mo
Prof.
Matr. 343/101
Correlatore Claudio
Iaselli
Dott. Ing. Giandomenico
a.a. 2004/2005
Nel presente lavoro di tesi, svolto nell’ambito di una ricerca teorico-sperimentale sulla dinamica dei motocicli da tempo in corso presso il DIME, è stata in particolare analizzata l’influenza della flessibilità strutturale sul fenomeno dinamico usualmente indicato con il termine “shimmy”, e la sua stabilità nei sistemi costituiti da ruote sterzanti, con particolare riferimento all’avantreno del motociclo.
Lo shimmy è un particolare fenomeno vibratorio che interessa le ruote sterzanti dei veicoli, le quali possono essere indotte, durante il loro moto di rotolamento, a seguire una traiettoria sinusoidale. Questo fenomeno è stato rilevato in diversi ambiti: dalle automobili ai carrelli di atterraggio degli aerei, dai carrelli portavivande ai rimorchi, dalle sedie a rotelle ai motocicli. I modi in cui lo shimmy si manifesta, e le cause che lo determinano, possono essere diversi, ed in taluni casi ancora non sono stati ancora del tutto interpretati.
Il fenomeno dello shimmy riguarda dunque sia coppie di ruote disposte su un asse comune, sia ruote singole, comunemente indicate con il termine caster; con tale denominazione si intende in particolare una ruota rotolante e sterzante, il cui punto di contatto con il piano strada giace posteriormente rispetto all’intersezione dell’asse di sterzo con il piano stesso.
Fino a
quando il piano della ruota è parallelo a quello longitudinale contenente la direzione del moto del telaio non si desta nessuna vibrazione, ma non appena un qualsiasi evento
causa una deviazione nella direzione delle ruote, ovvero si verifica una
accelerazione trasversale del telaio, si può verificare il fenomeno in esame.
Una volta che l’oscillazione di shimmy ha avuto origine, la sua ampiezza può
diminuire col tempo fino ad annullarsi, ovvero aumentare e persistere, a
seconda che ci si trovi in un campo rispettivamente di stabilità o instabilità
del sistema.
Secondo Roe, il motociclo può essere considerato costituito da una coppia di caster, vincolati mediante la cerniera di sterzo con asse inclinato. In questa ipotesi, il fenomeno dello shimmy è legato ad un particolare modo di vibrare dell’intero veicolo che va sotto il nome di wobble;
questo modo
consiste in oscillazioni dell’avantreno intorno all’asse di sterzo, e compare
usualmente
I primi studi sul fenomeno dello shimmy, condotti relativamente alle ruote anteriori degli autoveicoli e alle ruote dei carrelli di atterraggio degli aerei, prendevano in esame principalmente l’influenza della deformabilità dei pneumatici sulla instabilità delle oscillazioni. I risultati ottenuti con tale impostazione non potevano tuttavia spiegare l’oscillazione dei caster più semplici, come ad esempio quelli dei carrelli della spesa privi di pneumatici, né erano direttamente applicabili al problema della stabilità di un motociclo.
Roe afferma in particolare che la deformabilità del pneumatico è solo un aspetto particolare di un problema più generale di deformabilità laterale, che è la causa prima dell’instabilità del sistema. Per uno studio completo del fenomeno, è necessario quindi tenere conto, oltre che della rigidezza del pneumatico, anche della rigidezza strutturale dell’intero sistema, ovvero della ruota, del perno ruota e della forcella di supporto. Essendo la deformabilità del pneumatico fortemente smorzata, la rigidezza strutturale, ai fini dello studio del fenomeno, diventa particolarmente significativa nel caso dei motocicli, specialmente con il modello di forcella telescopico di supporto della ruota anteriore.
La teoria formulata da Roe spiega dunque l’origine del fenomeno in base alla capacità di deviazione laterale della superficie di contatto pneumatico-strada relativamente al piano individuato dall’asse di sterzo del motociclo e dalla direzione del moto di avanzamento della ruota.
La flessibilità laterale strutturale è simulata mediante due molle di rigidità k che contrastano il moto della ruota, supposta libera di spostarsi lateralmente all’interno della sua forcella di supporto.
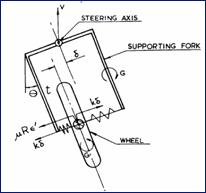
Figura 1 - Caster deformabile, asse di sterzo verticale
Viene esaminato il caso di asse di sterzo verticale, e successivamente quello di asse di sterzo obliquo, che fornisce un modello analitico più realistico per lo studio del problema della stabilità delle oscillazioni di shimmy di un motociclo, il cui asse di sterzo è inclinato di un angolo α ≠ 0.
Dalle simulazioni condotte dall’autore, effettuate variando di volta in volta i parametri del sistema, emerge che la stabilità delle oscillazioni dipende principalmente dal valore più o meno elevato della rigidezza strutturale. Allo scopo di indagare sull’influenza di quest’ultima sul fenomeno dello shimmy, e di effettuare un confronto con i dati presenti in letteratura, il problema è stato trattato secondo due diversi approcci, basati rispettivamente sull’integrazione numerica delle equazioni del moto, e su una modellazione di tipo multibody.
Per quanto riguarda il primo filone di indagine, si sono considerati due modelli di riferimento. Il primo modello preso in considerazione è il modello analitico di Roe: le equazioni differenziali del moto sono peraltro risultate in tal caso di difficile integrazione numerica. Si è quindi preso in considerazione un secondo modello più semplice, ed in particolare quello che va sotto il nome di classical shimming wheel di Stépán e Goodwine; è questo un modello meccanico più semplice, con numero ridotto di gradi di libertà, che tuttavia consente di mettere in evidenza il fenomeno dello shimmy, e fornisce risultati qualitativamente utili relativamente alla stabilità del fenomeno.
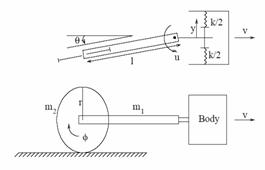
Figura
2 - Modello "classical shimmying wheel"
Il sistema è in questo caso modellato come un corpo rigido che avanza in rettilineo a velocità costante v. La ruota è rigida; la cerniera di sterzo è ad asse verticale, e può spostarsi solo ortogonalmente alla direzione del moto, essendo collegata al veicolo attraverso due elementi elastici lineari di rigidezza pari a k/2, che modellano la natura elastica del sistema. Il sistema, se si considerano solo i vincoli geometrici, ha tre gradi di libertà, corrispondenti all’angolo di rotazione φ della ruota, all’angolo di rotazione θ del caster rispetto alla direzione del moto, ed allo spostamento laterale y della cerniera di sterzo. Tale modello quindi, a differenza del modello di Roe che tiene conto anche dell’inclinazione dell’asse di sterzo, assume invece l’asse di sterzo verticale; il Roe, inoltre, considera anche la possibilità di uno spostamento relativo tra ruota e supporto, con cerniera di sterzo fissa.
I casi di rotolamento e di slittamento della ruota sono considerati separatamente.
Se si suppone
la forza di attrito sufficientemente grande da consentire un moto di puro
rotolamento, Stépán fornisce il sistema di equazioni differenziali ordinarie a
tre dimensioni θ, 
, y, che descrive il moto del sistema. La condizione di
stabilità è ricavata in funzione dei parametri geometrici ed inerziali, e non
dipende dalla velocità. Poiché però la forza di attrito ha una ampiezza
limitata, se la reazione del vincolo del contatto ruota-strada eccede questo
limite, il sistema può passare dalla
condizione di rotolamento
L’evoluzione
di questo sistema può essere rappresentata nello spazio delle fasi a 6 dimensioni
delle coordinate θ, , y, 
, φ, 
. A causa tuttavia della forte dissipazione dovuta
all’attrito coulombiano, la velocità relativa della ruota rispetto alla strada
nel punto di contatto diminuisce durante lo slittamento fino ad annullarsi; se
in questo istante la condizione di rotolamento è di nuovo soddisfatta, la ruota
ricomincia a rotolare. Quando è consentito il passaggio tra le due condizioni,
la dinamica del sistema evolve tra uno spazio delle fasi a quattro dimensioni
(condizione di puro rotolamento) ed uno a sei dimensioni (condizione di
slittamento).
Il modello è stato dunque analizzato considerando i due casi specifici di moto di puro rotolamento e di slittamento della ruota. In particolare, introducendo i parametri geometrici ed inerziali relativi all’avantreno dello scooter Scarabeo 150, si è rilevato che la condizione di stabilità del sistema in moto di puro rotolamento non è soddisfatta, e che quindi le oscillazioni in questo caso risultano sempre instabili.
E’ stato
anche valutato il valore di per il quale è
verificata la condizione prevista da Stépán relativa al passaggio del sistema
dal puro rotolamento allo slittamento. Individuati pertanto tale valore e
l’istante di tempo in cui la suddetta condizione si verifica, si sono valutati
i corrispondenti valori di θ, y, 
, φ e da fornire, per
assicurare la continuità, come condizioni iniziali per le equazioni che
descrivono il moto del sistema in condizioni di slittamento. E’ però necessario
sottolineare che, come si è già detto, al verificarsi di determinate
condizioni, risulta possibile che il sistema ritorni nuovamente nelle
condizioni di rotolamento; per questa ragione la dinamica è caratterizzata da
una continua evoluzione tra questi due stati. Queste particolari condizioni non
sono peraltro state prese in considerazione nel presente lavoro.
Sono state
effettuate numerose simulazioni in corrispondenza di tre valori di rigidezza di
ordine di grandezza differenti, e con valori crescenti della velocità. La
stabilità delle oscillazioni si verifica quando è presente una rapida
estinzione del transitorio, con oscillazioni stazionarie di ampiezza molto
piccola. Bisogna peraltro evidenziare che, anche se queste oscillazioni possono
apparentemente sembrare di piccola ampiezza, un wobble con oscillazioni di
ampiezza di 
risulta già molto
pericoloso.
Le simulazioni effettuate hanno messo in evidenza che, per bassi valori della rigidezza strutturale, si hanno elevate ampiezze di oscillazione; al contrario, per alti valori di tale parametro, risultano notevolmente ridotte sia la durata dei transitori sia le ampiezze dell’oscillazione stazionaria: viene pertanto confermata la rilevante influenza della rigidezza strutturale sulla stabilità del sistema.
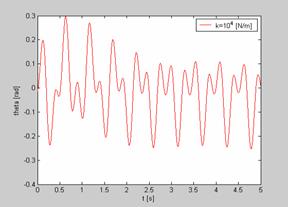
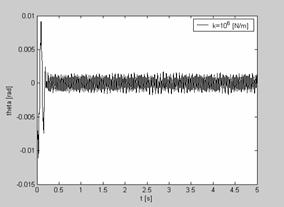
Figura 3-Time History di Theta (k=104,
v=20m/s) Figura 4-Time history
di theta ((k=106, v=20m/s)
Per quanto riguarda il secondo tipo di approccio al problema in esame, il modello multibody è stato messo a punto a valle della realizzazione di un modello CAD dell’avantreno dello scooter Scarabeo 150, fornito al DIME nell’ambito di uno studio condotto con Aprilia. Assegnate le condizioni di vincolo tra i componenti, le caratteristiche elastiche ed inerziali di questi ultimi, le azioni dinamiche agenti sul sistema e le condizioni iniziali del moto, si è quindi proceduto a due tipologie di simulazione di prova (su strada e al banco).
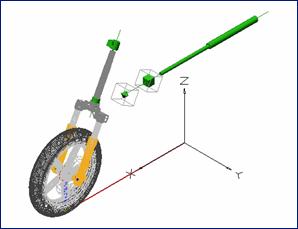
Figura 5 – Simulazione di prova su strada e al banco
In particolare, per quanto riguarda le azioni dinamiche agenti sul sistema, oltre alle azioni dovute al contatto tra pneumatico e strada, è stata considerata una forza applicata in corrispondenza della sommità del perno del cannotto di sterzo, per tener conto della presenza della parte di motociclo non presente nel modello. E’ stata inoltre introdotta una coppia agente sulla ruota che schematizza la resistenza al rotolamento.
Nel corso delle simulazioni sono state variate di volta in volta la velocità di avanzamento dell’avantreno ed il valore della rigidezza in direzione trasversale alla direzione di avanzamento.
In entrambi i casi, mediante l’utilizzo di vincoli opportuni, è stato possibile, oltre ad assegnare i valori di velocità di avanzamento e di rigidezza trasversale, applicare una coppia allo sterzo e registrarne la conseguente oscillazione. Si è in particolare valutata la risposta dinamica del sistema ad una coppia impulsiva allo sterzo, e sono state registrate le storie temporali di alcune grandezze caratteristiche. La scelta del tipo di impulso è dovuta al modo di vibrare che si è inteso esaminare: per evidenziare il wobble è infatti preferibile utilizzare una coppia impulsiva allo sterzo.
La rigidezza laterale dell’avantreno è stata schematizzata mediante una rigidezza concentrata che permette a tutto l’avantreno di traslare lateralmente. Questo tipo di schematizzazione dipende dal fatto che il codice multibody utilizzato non permette di associare a ciascun componente del sistema avantreno il corrispondente valore di rigidezza; tali componenti sono quindi stati considerati rigidi.
I risultati ottenuti risultano in buon accordo con quelli riportati da Roe, confermando il contributo decisivo alla stabilità del motociclo fornito da un elevato valore della rigidità trasversale dell’avantreno.
Nelle figure sotto riportate vengono mostrate due oscillazioni dello sterzo registrate a seguito dello stesso impulso di coppia e per uno stesso valore della velocità di avanzamento; k è la costante di rigidezza in direzione trasversale. Nel primo caso (k=250N/mm) il moto risulta evidentemente instabile, come si evince dal fatto che l’ampiezza delle oscillazioni diverge rapidamente, mentre nel secondo caso, con una rigidità trasversale k pari a 1000N/mm, il sistema risponde all’impulso di coppia stabilizzando il proprio moto dopo un breve transitorio.
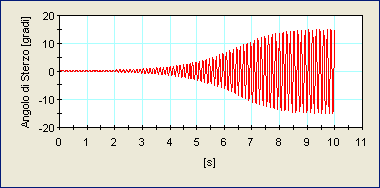
Figura 6 - Risposta dell'angolo di sterzo nel tempo (velocità = 20m/s, k = 250N/mm)
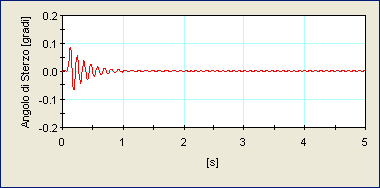
Figura 7 - Risposta dell'angolo di sterzo nel tempo (velocità = 20m/s, k = 1000N/mm)