Candidato: Francesco Timpone

Sommario della tesi di laurea dal titolo:

Modello FEM del forcellone posteriore del motociclo:
Influenza della struttura sul comportamento dinamico

Obiettivo della Tesi

In questa tesi si analizza la risposta dinamica strutturale di alcuni modelli tipici di forcellone posteriore di un motociclo, al fine di valutarne l’influenza sul comportamento dinamico complessivo di esso.

A tal proposito è stata utilizzata una metodologia basata sulla modellazione agli elementi finiti (FEM – Finite Element Method) mediante la quale ogni forcellone è stato caratterizzato dal punto di vista statico mediante la risposta all’applicazione di un carico di “flessione laterale” e di uno di “torsione” (questi schemi saranno precisati nel seguito), e dal punto di vista dinamico mediante la cosiddetta risposta “modale”.

Motivazioni

Nell’ambito del filone di ricerca sviluppato al DIME riguardante lo studio del comportamento dinamico del motociclo, sono stati effettuati studi riguardanti alcuni aspetti della dinamica longitudinale quali il comportamento nelle fasi di accelerazione [1,2] e la stabilità dell’ equilibrio nel moto rettilineo [3,4].

Fig. 1

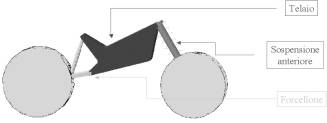
Quest’ultimo aspetto è stato peraltro oggetto di una precedente tesi di laurea [D’Aurea , Palumbo-“Sulla stabilità di un motociclo rispetto a perturbazioni laterali”] nella quale è stato utilizzato un modello Multibody del sistema (Fig. 1) costituito dalle seguenti parti, considerate rigide ed opportunamente vincolate: telaio principale, sospensione anteriore, forcellone posteriore e ruote.

Si è ritenuto che a questo stadio, un naturale sviluppo del modello fosse la rimozione del vincolo di rigidità delle parti forcellone posteriore in primo luogo e telaio principale nonché sospensione anteriore successivamente.

Infatti, se si analizza l’evoluzione dell’intera sospensione posteriore nella storia dei motocicli è evidente, già solo da un punto di vista architettonico, una notevole trasformazione strutturale (Fig. 2).

Gli schemi riportati, tranne in rare occasioni, sono quelli a cui, nel tempo, si sono sempre uniformemente adeguate le case motociclistiche. Pertanto, tali configurazioni, possono essere considerate dei milestones nello sviluppo della sospensione posteriore.

D’altra parte dall’indagine bibliografica svolta sono emerse ragioni sia tecniche che tecnologiche di quest’evoluzione quali ad esempio:

· La necessità di avere curve cosiddette “progressive” della rigidezza della sospensione (ridotta all’asse ruota)

· Aumentare l’escursione massima della ruota

· Diminuire la massa non sospesa

Fig. 2

Parallelamente all’evoluzione dell’intera sospensione posteriore ed in maniera forse ancorpiù marcata dal punto di vista architettonico, si è evoluto il componente forcellone. A prescindere anche dall’evidente differenza tra le soluzioni bi-braccio e monobraccio, questa complessità evidenzia una notevole evoluzione dal punto di vista strutturale.

Inoltre le varie configurazioni in cui lo si ritrova negli attuali motocicli sono fortemente orientate dal tipo di uso prevalente del motociclo: si passa da forcelloni a semplice struttura costituita da tubi di ridotta sezione circolare d’acciaio per motocicli di impiego prevalentemente cittadino a tubi scatolari di più grande sezione d’acciaio per veicoli da fuoristrada ed infine a tubi scatolari di grande sezione di alluminio con capriate di irrigidimento per veicoli da strada di elevate prestazioni e da competizione su pista (Fig. 2).

Diversamente da quanto trovato a proposito dell’intera sospensione posteriore, l’indagine bibliografica effettuata non ha chiarito le ragioni della tendenza verso configurazioni a struttura così complessa.

Pertanto con questa tesi si è iniziata una fase di indagine in tal senso.

Sviluppo ed organizzazione della tesi

La tesi è stata organizzata in quattro capitoli.

Nel primo di questi si riportano le nozioni generali riguardanti il funzionamento della sospensione posteriore dei motocicli e vengono analizzati i differenti comportamenti al variare della configurazione.

Il capitolo 2 riguarda la modellazione FEM di strutture ed in particolare si sofferma sugli aspetti riguardanti la risposta dinamica.

Nel capitolo 3 si descrivono in dettaglio le modalità con cui si è affrontata la costruzione dei modelli di forcellone e si definiscono le condizioni di carico statico.

Nel capitolo 4, infine, si riportano i risultati delle analisi statiche e dinamiche effettuate per ogni modello e le conclusioni della tesi.

Risultati e conclusioni

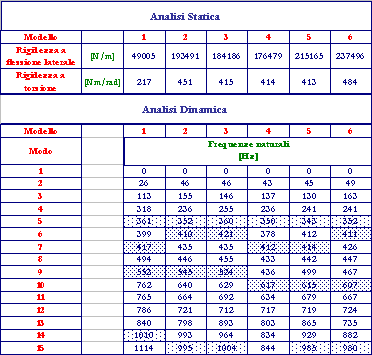
L’analisi statica ha consentito di caratterizzare ogni forcellone mediante i due parametri “rigidezza laterale” e “rigidezza torsionale” (

Fig. 3). Successivamente è stata condotta l’analisi dinamica ricavando per ogni modello i primi 15 modi naturali, le cui frequenze sono comprese tra 0 e 1 kHz.

Fig. 3

Tale campo di frequenze contiene quello delle forzanti derivanti dalla percorrenza di superfici stradali mediamente rugose, con velocità di avanzamento comprese tra 0 e 80 ms^-1 []; inoltre comprende senz’altro il campo di frequenze naturali del sistema cerchio ruota-pneumatico.

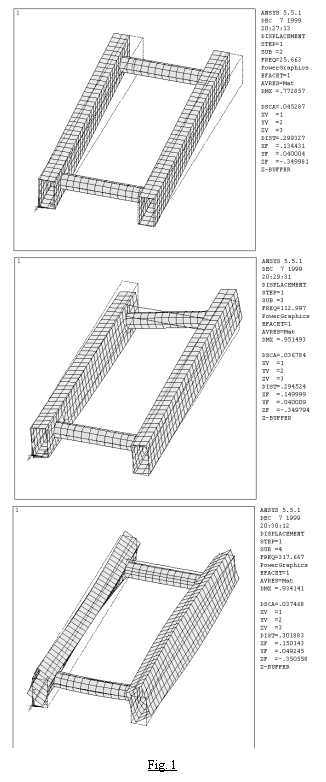Casella di testo:
Fig. 4 In Fig. 4 sono riportate le deformate dei primi 3 modi del modello 1 di forcellone (in alluminio e senza capriata di irrigidimento).

Tali deformate si presentano geometricamente simili per i 6 modelli di forcellone analizzati; viceversa a partire dal 4° modo in poi, non c'è più corrispondenza tra numero del modo e deformata per i diversi modelli: ciò è naturale se si pensa già al solo fatto che i diversi modelli hanno un differente numero di gradi di libertà.

Si è resa necessaria allora la ricerca di un criterio, non semplicemente basato sull'ordinamento dei modi in base alla loro frequenza, per l'individuazione di modi "ingegneristicamente" confrontabili.

Tab. 1