Testi delle prove intercorso
di Meccanica delle vibrazioni
Prova intercorso del 22.1.2001
q Domanda
n. 1
Esporre la teoria degli
accelerometri sismici, descrivendo quelli di tipo piezoelettrico.
q Domanda
n. 2
Esporre e dimostrare
il teorema dell’ortogonalità dei vettori colonna.
q Domanda
n. 3
Per il “quarter model” di un autoveicolo, rappresentato dallo
schema in figura, che trasla con velocità V costante mantenendosi
in posizione verticale, la cui ruota (perfettamente rigida) rotola senza
slittamento su un profilo stradale sinusoidale, disegnare il bond graph
completo del modello dinamico.
q Domanda
n. 4 (facoltativa)
Per il sistema dell’esercizio precedente, determinare
il valore della rigidità della sospensione per cui l’accelerazione
della massa (sospesa) m sia inferiore al 10% dell’accelerazione
verticale della ruota, nell’ipotesi semplificativa che lo smorzamento s
dell’ammortizzatore sia nullo.
|
m
|
250
|
kg
|
|
V
|
30
|
ms-1
|
|
l
|
3 p
|
m
|
|
Z0
|
0.05
|
m
|
Prova intercorso del 19.2.2001
Esporre la teoria degli smorzatori
dinamici, descrivendone i pi¨ comuni esempi di applicazione.
Esporre e dimostrare il teorema di
espansione.
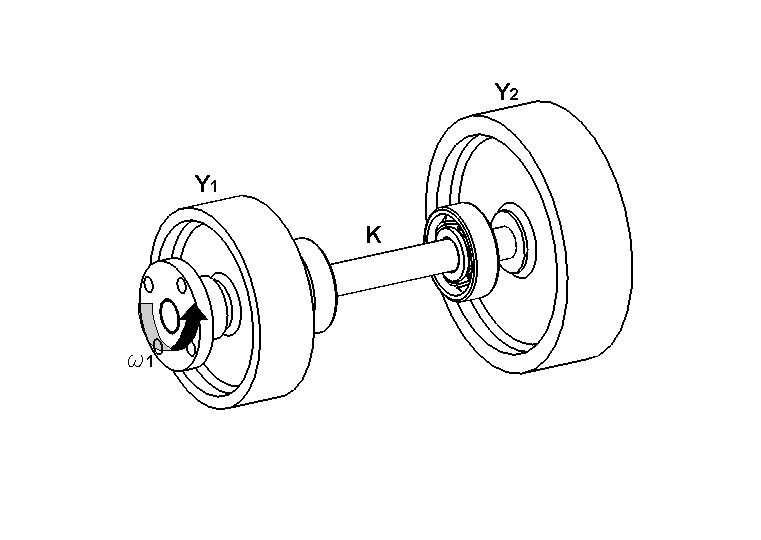
Al giunto di accoppiamento del
sistema rappresentato nello schema in figura, infinitamente rigido e rigidamente
vincolato al volano Y1, Ŕ imposto un moto rotatorio con
un’assegnata legge di velocitÓ w 1=w
1(t); disegnare il bond graph completo del modello dinamico
torsionale, ed individuare l’ordine del modello nonchÚ le sue variabili di
stato.

- Domanda n. 4. (facoltativa)
Per il sistema dell’esercizio
precedente, nell’ipotesi che il giunto abbia una rigiditÓ torsionale finita KG,
disegnare il nuovo bond graph, individuare l’ordine del modello nonchÚ le sue
variabili di stato, e descrivere le eventuali variazioni del comportamento del
modello rispetto al caso dell’esercizio precedente.
Prova intercorso del 21.1.2002
ě
Domanda n. 1
Moto forzato di un sistema
massa-molla a due gradi di libertÓ dovuto ad azione forzante armonica agente su
una delle due masse.
ě
Domanda n. 2
Moto forzato di sistemi
conservativi a n gradi di libertÓ in presenza di azioni forzanti armoniche e
sincrone.
ě
Domanda n. 3
Il
sistema in figura rappresenta un rotismo riduttore ottenuto bloccando la ruota
solare A di un rotismo epicicloidale. Al giunto di accoppiamento Ŕ applicata la
coppia motrice Mm=Mm(t), mentre sull’albero del
portatreno P Ŕ calettato un volano di momento d’inerzia di massa Y. Disegnare
il bond graph completo del suddetto modello nelle ipotesi che il giunto di
accoppiamento e tutti gli alberi siano infinitamente rigidi torsionalmente e le
inerzie di tutte le parti mobili,
eccetto il volano Y, siano trascurabili. Effettuare le opportune considerazioni
sull’ordine del modello e sulla possibilitÓ di effettuarne l’integrazione
numerica con metodi a passo fisso o variabile.


ě
Domanda n. 4. (facoltativa)
Per il sistema
dell’esercizio precedente, disegnare il bond graph nel caso in cui si voglia
tener conto anche dei seguenti parametri:
ž
rigidezza finita KP dell’albero del portatreno su cui
Ŕ calettato il volano
ž
rigidezza finita KB dell’alberino della ruota B
ž
rigidezza finita Kg del giunto di accoppiamento
ž
rigidezza finita Ks dell’alberino portasatelliti
ž
momenti d’inerzia di massa YA, YB, YC,
YD, delle ruote, YP, del portatreno
ed
effettuare le stesse considerazioni richieste nell’esercizio precedente.
___________________________________________________________________________
Prova intercorso del
18.2.2002
ě
Domanda n. 1
Descrivere il
funzionamento degli smorzatori dinamici Stockbridge per cavi di alta tensione e
spiegarne i criteri di proporzionamento.
ě
Domanda n. 2
Sistemi conservativi a n
gradi di libertÓ: il problema degli autovalori e degli autovettori.
ě
Domanda n. 3
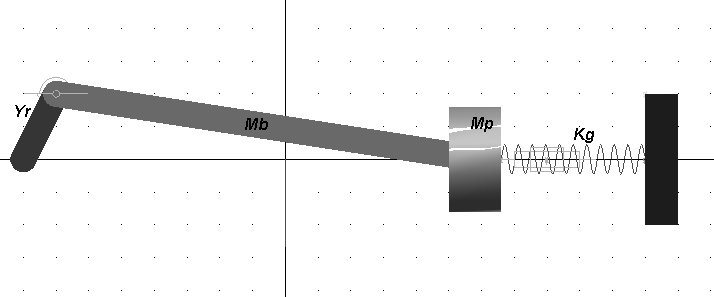
Per il meccanismo
schematizzato in figura, soggetto ad una coppia M=M(t)
applicata alla manovella, disegnare il modello bond graph completo, ed
effettuare le opportune considerazioni relative all’ordine del modello,
all’eventuale presenza di variabili di stato dipendenti, ecc. Si considerino
le masse ridotte del sistema, al baricentro del pistone ed al bottone di
manovella.
ě
Domanda n. 4. (facoltativa)
Per
il meccanismo di cui alla domanda precedente, rispondere alle stesse domande
sostituendo alla coppia M=M(t) agente sulla manovella l’imposizione di una
legge di velocitÓ angolare w=w(t).
___________________________________________________________________________
Prova
intercorso del 22.1.2003
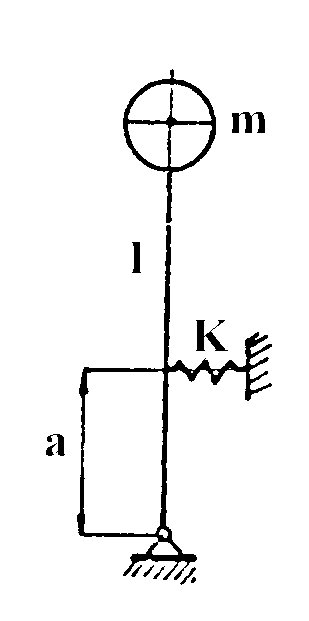 Descrivere
il comportamento dinamico del pendolo capovolto elasticamente vincolato
rappresentato in figura.
Descrivere
il comportamento dinamico del pendolo capovolto elasticamente vincolato
rappresentato in figura.
ě
Domanda n. 2
Spiegare
il comportamento degli smorzatori dinamici, esemplificando lo scopo, il
funzionamento ed il proporzionamento di quello automobilistico.
ě
Domanda n. 3
Descrivere
e dimostrare le caratteristiche peculiari dei sistemi semidefiniti.
ě
Domanda n. 4. facoltativa
(da trattare eventualmente solo dopo le domande 1-3)
Per
il rotismo differenziale il cui schema Ŕ rappresentato in figura, Ŕ
rappresentato il relativo modello Bond Graph. Mediante l’analisi di causalitÓ
applicata a quest’ultimo effettuare le opportune considerazioni ed i confronti
dei modelli nei casi in cui:
1.
Al portatreno P Ŕ applicata una coppia;
2.
Al portatreno P Ŕ applicata una coppia e ad una delle ruote A o B Ŕ imposta
una velocitÓ angolare.

___________________________________________________________________
Prova
intercorso del 17.2.2003
ě
Domanda n. 1
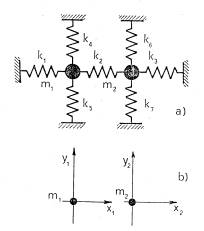 Per
il sistema rappresentato in figura, con:
Per
il sistema rappresentato in figura, con:
m1
= m2 = 1.0 kg
K1
= K2 = K5 = 6000 Nm-1
K3
= K4 = K7 = 8000
„
K6
= 4000
„
determinare
le pulsazioni naturali e le corrispondenti deformate nell’ipotesi di rigiditÓ
laterali delle molle uguali a zero.
ě
Domanda n. 2
Sistemi conservativi a
n gradi di libertÓ: determinazione del moto libero di assegnate condizioni
iniziali.
ě
Domanda n. 3
Descrivere il
funzionamento dei vibrometri sismici.
ě
Domanda n.4. facoltativa (da trattare eventualmente solo dopo
le domande 1-3)
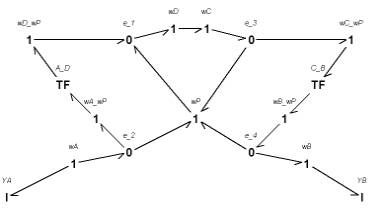
Per il rotismo
differenziale il cui schema Ŕ rappresentato in fig. 1, Ŕ rappresentato il
relativo modello Bond Graph in fig.2. Mediante l’analisi di causalitÓ
applicata a quest’ultimo effettuare le opportune considerazioni ed i confronti
dei modello nei casi in cui:
1.
Al portatreno P Ŕ applicata una coppia;
2.
Al portatreno P Ŕ applicata una coppia ed ad una delle ruote A o B Ŕ
imposta una velocitÓ angolare

___________________________________________________________________
Prova
intercorso del 26.2.2004
ě
Domanda n. 1
Dimostrare il Teorema di Espansione e spiegarne
l’utilizzazione nel metodo dell’Analisi Modale.
ě
Domanda n. 2
Dinamica di un corpo rigido elasticamente sospeso:
sistema di riferimento, matrice [m] e matrice [K].
ě
Domanda n. 3
Descrivere il funzionamento dello smorzatore dinamico
per uso automobilistico, e spiegarne i criteri di proporzionamento.









 Descrivere
il comportamento dinamico del pendolo capovolto elasticamente vincolato
rappresentato in figura.
Descrivere
il comportamento dinamico del pendolo capovolto elasticamente vincolato
rappresentato in figura.

 Per
il sistema rappresentato in figura, con:
Per
il sistema rappresentato in figura, con: