Acids and bases

In this section we shall deal with solutions containing a mixture of an acid (AH) and a base (BOH). In such solutions reactions 1-5 take place

1. Acid dissociation	2. Base dissociation	3. Neutralization
AH + H2O  H3O+ + A-	BOH + H2O  OH- + B-	H+ + OH- --> H2O

4. Hydrolysis of A-	5. Hydrolysis of B-
A- + H2O  AH + OH-	B- + H2O  BOH + H+

It follows that the pH of a solution containing an acid and a base depends on the respective amount of the two components (neutralization reaction) and on their ability to react with water (hydrolysis).

The most simple case: reaction of a strong acid with a strong base.

In this case neither B⁺ or A^- (arising from the full dissociation of the acid and the base respectively) can react with water, thus only the reaction of neutralization has to be considered.

Here follows the possible cases:

For nAH = nBOH, pH = 7	In fact all H+ and OH- are transformed in water through the neutralization reaction.
For nAH > nBOH, pH < 7	Only the excess of the acid (nAH - nBOH) is to be considered
nAH < nBOH, pH > 7	Only the excess of the base (nBOH-nAH) is to be considered

A more involved case: reaction of a weak acid with a strong base (or vice versa).

All the examples reported here, refers to a weak acid and a strong base. However, the reader should realize that problems involving a weak base and a strong acid are perfectly equivalents.

In a solution containing a weak acid and a strong base only the reactions 1-4 should be considered in fact B^- (arising from a strong base) can not hydrolyze.

1. Acid dissociation	2. Base dissociation	3. Neutralization
AH + H2O  H3O+ + A-	BOH + H2O  OH- + B-	H+ + OH- --> H2O

4. Hydrolysis of A-	5. Hydrolysis of B-
A- + H2O  AH + OH-	B- + H2O  BOH + H+

In principle, in order to calculate the pH of a such solution we should consider all the equilibria, but we will see that reasonable approximations can be made to solve the problem. Let's consider the differents cases: 

[base] > [acid]

In this case the acid will be full converted in its conjugate base (neutralization reaction, 3), thus we should consider only the reaction of hydrolysis (4). However, the presence of an excess of OH^-, arising from the full dissociation of the base, will repress the reaction of hydrolysis according to LeChatelier' s principle (the common ion effect). Therefore, we can calculate the pH by considering only the excess of the base.

[base] = [acid]

The case of solution in which [base] = [acid], is perfectly equivalent to a solution of the salt formed by the acid and the base. For example, a solution containing 0.5 moles of acetic acid and 0.5 moles of NaOH in one liter of water, is perfectly equivalent to a 0.5 M solution of sodium acetate. In this case the only reaction one should consider is the hydrolysis reaction of the weak component (4). The hydrolysis constant (5)

[AH] [OH^-]
5. K_i = -----------
[A^-]

can be simplified by assuming that

[AH] = [OH^-] i.e., we neglect OH^- contributed from water;

[A^-] = Cs (initial concentration of the salt), i.e., we neglect the small amount of A- which hydrolizes.

Therefore, the hydrolysis constant can be written as in 6 and remembering that K_i = Kw/Ka, we obtain equation 7.

[OH-]2 6. Ki  = ------- Cs

CsKw 7. [OH-]2 = ----- Ka

Taking -Log:

pOH = 1/2 pKw - 1/2 pKa - 1/2 Log Cs

pH =  pKw - pOH = pKw - (1/2 pKw - 1/2 pKa - 1/2 Log Cs)

pH = 1/2 pKw + 1/2 pKa + 1/2 Log Cs

It should be evident that in the case of a weak base and a strong acid we should consider the hydrolysis constant of the base and follow the same reasoning made above.

Solutions containing an excess of a weak acid with respect to a strong base (or viceversa) deserves more attention for they have the property to minimize change in pH when small amounts of an acid or a base is added to them (buffers). Let' consider the case in which the acid is in excess with respect to the base (we still remember that the treatment of a solution containing a weak base in excess with rispect to a strong acid is perfectly equivalent), such solution will contain both an appreciable amount of

AH  (the undissociated acid, which also arises from hydrolysis reaction)

A^- (the conjugated base produced by neutralization and dissociation reactions)

Therefore, in order to calculate the concentrations of AH and A^- we should consider the following equilibria: dissociation, hydrolysis and neutralization. However, we can simplify the problem by making the following considerations according to LeChatelier's principle (the common ion effect):

In a weak acid solution, only a very small amount of the acid is dissociated. Furthermore, the presence of an appreciable amount of its conjugated base (produced by the base) further repress the dissociation. Thus it can be assumed, with a good approximation, that at equilibrium [A^-] = the concentration of the strong base added;

In a pure solution of a conjugated base of a weak acid only a small fraction reassociate and the presence of appreciable amount of the acid further repress the hydrolysis reaction. Thus it can be assumed, with a good approximation, that at equilibrium [AH] = [AH] _initial - the concentration of the strong base added.

 

Example 1. Preparation of 1 liter of a sodium acetate buffer 0.1 M, pH 5. First we note that the concentration of a buffer refers, generally, to the analytical concentration of the weak component. In this case 0.1 M is the sum of [CH3COOH] and [CH3COO-]. The most simple procedure to prepare this buffer is to dissolve 0.1 moles of acetic acid in about 900 milliliters of water add enough NaOH to reach pH 5. add enough water to reach one liter of solution. This is the most simple procedure if we can measure the pH (e.g., with a pH-meter) of the solution during the addition of the base. If a pH-meter is not available, we can use the Henderson-Hasselbach equation to calculate the amount of NaOH (indicated with x) needed to reach pH 5 (see 1-7). Example 2. Let's see as the same buffer can be prepared using sodium acetate and acetic acid. According to the calculations made above we need to add 0.064 moles of NaOH to the acetic acid solution and thus [CH3COOH] = 1 - 0.064 = 0.036. Therefore, [NaOH] = [CH3COO-] = 0.064 [CH3COOH] = 0.036 If we dissolves 0,064 moles of sodium acetate and 0.036 moles of acetic acid in 1 liter of water, we have that [CH3COO-] = 0.064 in fact, salts are strong electrolytes (i.e. full dissociated). [CH3COOH] = 0.036 in fact, due to the presence of acetate no appreciable dissociation of the acid will occur. For this reason you can find the equation of Henderson-Hasselbach written as in 8.

[CH3COOH] 1. pH = pKa - log --------- [CH3COO-] [CH3COOH] 2. 5 = 4.75 - log ---------- [CH3COO-] 0.1 - x 3. 4.75 - log ---------- = 5                    x 0.1 - x 4. log ---------- = 0.25 x 0.1 - x 5. ---------- = 10 - 0.25 = 0.56 x 6. 0.1 = 0.56x + x = x(0.56 + 1) 7. x = 0.1/1.56 = 0.064 moles of NaOH Ca 8. pH = pKa - Log ------ Cs Ca is the concentration of the acid. Cs is the concentration of the salt.

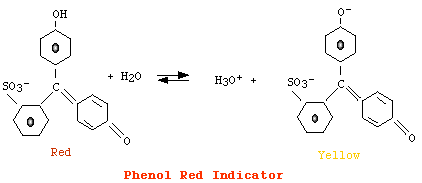Earlier on these page we have described the titration of Cl^- with AgNO₃ using chromate as indicator of endpoint of the titration. In the case of acid-base reactions the monitoring of pH can be used to establish the endopoint of the titration. The most simple acid-base titration is that involving a strong acid and a strong base (e.g., HCl and NaOH). Since neither Na⁺ or Cl^- can hydrolyze, the endpoint of the titration is indicated by pH = 7. At this pH, the number of moles of the base is equal to those of the acid (equivalence point) and the concentration of the unknown can be calculated from the volume of titrant added. In the case of a titration involving a weak acid with a strong base or a strong acid with a weak base the hydrolysis phenomen should be taken in account and the equivalence point, will be at pH >7 when a weak acid is used and at pH <7 when a weak base is used. The simplest way of estimating the pH of a solution is provided by the so called indicators. These are weak acids or bases whose respective conjugate forms have a different color. The color of a solution containing an indicator depends on the ratio of conjugate forms, i.e., on pH value:
 

AH + H2OA- + H3O+

[AH] pH = pKa - Log -------                 [A-]

For phenol red [AH] > [A-], color = red [A-] > [AH], color = yellow

However, since eye can detect changes in color only when the concentration of a form is ten fold the concentration of its conjugate, we have that:

the color corresponding to [AH] is detected when pH = pKa + Log (0.1) i.e., when pH = pKa - 1

the color corresponding to [A^-] is detected when pH = pKa + Log (10) i.e., when pH = pKa + 1