 H+ + OH-
H+ + OH-
Water is a weak electrolyte which dissociates as follows:
H2O  H+ + OH- H+ + OH- |
K = [H+] [OH-]/[H2O] |
Because only a very small amount of water dissociates, the concentration of H2O (about 55 M) can be considered constant and included in K. The new constant, generally indicated as Kw, is known as the ion product of water and at 25 oC is equal to 10-14.
K [H2O] = [H+] [OH-] = Kw = 10-14
From the stoichiometry of the reaction it results that [H+] = [OH-] = 10-7. This equation also results from the observation that solutions are electrically neutral, thus the concentration of positive charge must equal the concentration of negative charge. The equation [H+] = [OH-] thus represents the charge balance equation for pure water.
For reason of compactness and brevity, chemists prefer to express concentrations in terms of their negative decimal logarithms. Taking -Log [H+] and indicating -Log with p we have, in pure water:
pH = - Log [H+] = - Log 10-7 = 7
thus pH is merely the -Log10 [H+] and the pH of pure water is 7. Please note that -Log10 [H+] is equivalent to Log10 1/[H+]
Let's consider again the ion product of water:
Kw = [H+] [OH-] = 10-7. 10 -7 = 10-14
Taking -Log and remembering that in chemists notation the symbol p indicates -Log:
-Log Kw =-Log [H+] - Log [OH-] = - Log 10-14 = 14pKw = pH + pOH = 14
For pure water [H+] = [OH-] thus pH = pOH = 7.
A solution having pH = 7 (and of course pOH = 7 ) is said neutral.
A solution with pH < 7 is said acid while a solution with pH > 7 is said basic or alkaline.
Values of pH can be measured with commercial instruments (pH-meters) with an accuracy of ±0.01 pH units. The description of this instrument is beyond the scope of these pages.
|
Introduction
|
The classification of substances as acids was at first suggested by their sour taste (Latin acidus = sour; acetum = vinegar). Alkalis (Arabic al kali = ashes of a plant) were taken as those substances that could reverse or neutralize the action of acids. It was also believed that oxygen is a necessary constituent of acids (Greek oxus = sour; gennae = I produce). After Davy, that in 1810 demonstrated that hydrochloric acid contained only hydrogen and chlorine, hydrogen was taken as an essential constituent of acids.
According to Arrhenius theory, the proton (H+) is responsible for acidic properties while the hydroxyl ion (OH-) is responsible for basic (alkaline) properties.
Acids are thought as compounds which dissociate giving a proton (and its counter ion) such as:
HCl = H+ + Cl-CH3COOH = H+ + CH3COO-
Bases are thought as compounds which dissociate giving an hydroxyl ion (and its counter ion) such as:
NaOH = Na+ + OH-
Limits of Arrhenius theory can be summarized as follow:
There are many evidences indicating that proton does not exist free in aqueous solution but it is bound to water (hydrated). Normally this hydrated proton is indicated as H3O+ (hydronium ion) but this is a simplification because this ion is further hydrated (H9O4+). According to these observations acids can be thought as compounds able to donate (transfer) protons to other molecules rather than compounds dissociating to protons (Arrhenius theory): HCl + H2O = H3O+ + Cl-The Arrhenius theory can not explain, for example, the observation that ammonia is a base and carbon dioxide is an acid. In fact, these two compound cannot dissociate directly to give an hydroxyl and a proton (H+) respectively.
The considerations above, led Lowry-Bronsted (1923) to propose a more general concept of acids and bases.
|
Lowry-Bronsted theory
|
Arrhenius
|
| Acids are substance having the tendency
to donate a proton to another molecule;
Bases are substance having the tendency to accept a proton from another molecule. Thus an acid exists if exists a compound which accepts a proton (i.e., a base) and a base exists if exists a compound which donates a proton (i.e., an acid). CH3COOH + H2O = H3O+ + CH3COO- the acidity of acetic acid is due to the reaction between an acid (acetic) and a base (water). |
The acidity of acetic acid is due to its dissociation in hydrogen and acetate ions. CH3COOH = H+ + CH3COO-
|
The reaction between acetic acid and water is reversible i.e., acetate ion can accept the proton from the hydronium ion to give back acetic acid:
H3O+ + CH3COO- = CH3COOH + H2O
Therefore, acetate ion is a base and H3O+ is an acid.
According to this observation, Lowry-Bronsted theory introduced the concept of conjugate acid-base pairs:
Acetate and acetic acid are conjugated acid-base pairs.water and hydronium ion are conjugated acid-base pairs.
Eventually, while the Arrhenius theory cannot explain the fact that ammonia is a base, Lowry-Bronsted theory can:
NH3 + H2O = NH4+ + OH-
The base ammonia can accept a proton from the acid water thus giving rise to an increase of OH- in solution.
In the Arrhenius theory, the fact that acids and bases have different strength is the result of a different degree of dissociation. Therefore,
HCl which is a strong electrolyte (fully dissociated) is a strong acid;Acetic acid which is a weak electrolyte (partially dissociated) is a weak acid.
In the Lowry-Bronsted theory, the strength of an acid is its tendency to transfer a proton and the strength of a base is its tendency to accept protons.
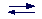
Strong acids (bases) are those for which the reaction is complete, i.e., there is no equilibrium between the species in solutions (indicated by a right arrow):
HCl (acid) + H2O (base) --> H3O+ (acid) + Cl- (base)
It is worth noting that water can act as an acid and as a base. Substances like water are said ampholytes (amphoteric compounds). It follows that the reaction of dissociation of water should be more correctly written as
H2O + H2O
H3O+ + OH-
On the contrary, weak acids and bases are those compounds for which the transferring of proton is not complete. Examples of weak acids are acetic and formic acids
CH3COOH + H2OH3O+ + CH3COO-
Keq = 1.8 x 10-5, pKa = 4.76HCOOH + H2OH3O+ + HCOO-
Keq = 1.8 x 10-4, pKa = 2.93
Formic acid is stronger than acetic acid as results from its Ka: the higher Ka, the stronger the acid, or the lower pKa, the stronger the acid.
An example of weak base is ammonia:
NH3 + H2ONH4+ + OH-
The reaction of the conjugated base (acid) of a weak acid (base) with water is indicated as hydrolysis. Consider the dissociation of acetic acid:
| equ 1. CH3COOH + H2O |
The formed acetate ion can react with water (hydrolysis) as shown in equ 2:
| equ 2. CH3COO- + H2O |
It should be evident that Kb it is the reciprocal of the ionization constant (ka).
By multiplying Ka with Kb and eliminating the concentration of acetate and acetic acid we obtain
Ka Kb = [H+] [OH-] = 10-14
and taking -log it results that
pKa + pKb = 14
where pKa and pKb stands for -log Ka and -log Kb respectively
The understanding of the hydrolysis phenomenon is very important to deal with calculation of pH of mixtures of acids and bases. Let's consider here, the case of salts. Salts can be thought as the result of the reaction between acids and bases and they differ for the nature (strong or weak) of their components. For example,
Sodium Acetate (CH3COONa) is an example of salt formed by a weak acid (acetic acid) and a strong base (NaOH). This salt when dissolved in water fully dissociates in acetate and sodium ions. However, the acetate ion, the conjugated base of acetic acid (a weak acid), can hydrolyze (equ 2 ) leaving an excess of OH-. Thus a solution of such kind of salts (weak acid-strong base) will be basic (pH > 7).
Ammonium Chloride is an example of salts formed by a strong
acid and a weak base. The ammonium ion, the conjugated base of NH3
(a weak base), can hydrolyze (NH4+ + H2O ![]() NH3 + H3O+). Thus a solution of such kind of
salts will be acid (pH < 7).
NH3 + H3O+). Thus a solution of such kind of
salts will be acid (pH < 7).
Ammonium Acetate is an example of salts formed by a weak acid and a weak base. Therefore, both the ions can undergo to the hydrolysis reaction. As a consequence, the variation in pH will depend on the relative strength of the two components.
Sodium chloride (NaCl) is an example of salt formed by a strong acid and a strong base. Because neither Na+ nor Cl- can undergo hydrolysis, the dissolution of such kind of salts will not produce any variation in pH. Therefore a solution of NaCl is neutral (pH = 7).
In conclusion, the pH of a salt solution depends on the nature of the base and acid forming the salt, i.e., on their ability to react with water (hydrolysis).
In a solution of an acid in water there are two source of hydrogen ions: the acid and water. However, the concentration of hydrogen ions contributed by water dissociation is very small. It is 10-7 for pure water but it will be less than 10-7 when an acid is added (according to LeChatelier's principle). Thus, in most of cases this concentration can be neglected and only the concentration of the acid is considered. Let's consider a solution obtained by adding 0.1 moles of HCl to 1 liter of water. This solution is 0.1 M in HCl and since a strong acid is fully dissociated the solution is also 0.1 M in hydrogen ions, thus pH = - Log(0.1) = 1. In the case of a strong base the concentration of OH- contributed by water dissociation can be neglected (for the same reasons discussed above) and thus pOH = - Log(0.1) = 1. Remembering that pH + pOH = 14, pH = 14 - 1 = 13.
Let's calculate the pH of a solution of HCl 10-8 M. According to what said above it will be pH = - Log [H+] = - Log 10-8 = 8. Of course this is a nonsense result for a solution of an acid must have a pH < 7. This result is due to the fact that in a very diluted acid solution the [H+] contributed by water cannot be neglected. Thus the pH of a such solution should be calculated by taking in account both the [H+] contributed by water and the acid. In order to solve this problem we will use two laws of conservation:
Conservation of charge. Charge can not be created or destroyed. Since water is electrically neutral, negative charges must equal positive charges (equ. 1 and 2). When an acid (e.g., HCl) is added equ. 3 will hold.
| 1. H2O = H+ + OH- | 2. [H+] = [OH-] | 3. [H+]water + [H+]HCl = [OH-]water + [Cl-]HCl |
Conservation of Mass. Mass can not be created or destroyed, thus in the case of HCl dissociation (HCl = H+ + Cl-), equations 4 and 5 will hold:
4. [HCl]initial = [HCl]residue + [Cl-]dissociated
5. [HCl]initial = [HCl]residue + [H+]dissociated
In this particular case, i.e., the case of a strong electrolytes, [HCl]residue is 0 and then [Cl-] = [H+] = 10-8. By inserting this value in the charge balance equation, we have
[H+]water + 10-8 = [OH-]water + 10-8
From this last equation it should be evident that, when the acid is added, [H+]water is still equal to [OH-]water. Indicating these two concentrations with x, the ion product constant for water becomes
[H+][OH-] = (10-8 + x) * x = 10-14; x2 + 10-8x - 10-14 = 0
solving this quadratic equation we obtain x= 9.5 10-8. Thus the total concentration of H+ is 10-8 + 9.5 10-8 = 10.5 10-8 which corresponds to pH 6.98.
Let 's consider now the case of solutions of weak acids or weak bases. This is a more involved problem and we begin to describe an approximate procedure to obtain the pH of these solutions. As in the case of strong acids we consider that H3O+ contributed by water is very small and it can be neglected. In other words, we assume that in the equilibrium constant [A-] = [H3O+]:
| 1. AH + H2O |
Furthermore, we assume that the amount of the dissociated acid is very small, so the concentration of the acid at equilibrium can be considered equal to the initial concentration of the acid (Co):
| 5. [H3O+] = (Ka Co)1/2 |
Taking -Log of equation 5 we have an expression to calculate the pH:
| 6. pH = 1/2 (- Log (Ka) - Log Co) | 7. pH = 1/2 (pKa - Log Co) |
A similar equation for pOH can be deduced in the case of a weak base and the pH can be calculated from the equation pH + pOH = 14.
Let's see now if the assumptions made to calculate the pH of a weak acid solution are always justified. In equ. 8, 9 and 10 are reported the [H+] and pH of three different solutions of acetic acid (Ka = 1.85 X 10-5 and pKa = 4.75) calculated by equ. 5:
| 8. 1 M acetic acid | [H+] = 4.3 X 10-3 | pH = 2.37 |
| 9. 0.01 molar acetic acid | [H+] = 4.3 X 10-4 | pH = 3.37 |
| 10. 0.001 molar acetic acid | [H+] = 1.36 X 10-4 | pH = 3.87 |
In all three cases, the assumption that [H+] contributed by water (less than 10-7) is small compared to that contributed by the acid is justified. In practical cases [H+] contributed by water can be neglected.
The other assumption made to calculate pH was that the amount of acid dissociated is small compared to the initial concentration of the acid. From the concentration of [H+] reported in 8, 9 and 10 we can calculate the percent of acid dissociated:
| 1 M | [H+] is 0.43% of the initial concentration |
| 0.01 M | [H+] is about 4% of the initial concentration |
| 0.001 M | [H+] is about 13% of the initial concentration |
Thus, the second assumption deserves much more attention that the first one. In fact, the amount of the dissociated acid depends both on the initial concentration of the acid and on its dissociation constant. Two different approaches can be used to deal with this problem. As first, we can use the accurate relation in which the concentration of the acid at equilibrium is equal to the difference between the initial concentration of the acid (Co) and the aliquot dissociated (which is equal to the concentration of H3O+ at equilibrium). Therefore we obtain a quadratic equation:
Applying this equation to the case of a solution 0.001 M of acetic acid, we can calculate that [H3O+] = 1.27 x 10-4 (the approximate concentration previously calculated was 1.36 x 10-4, i.e., 7% more of the accurate concentration).
Alternatively, we can use the approximate concentration of H3O+ to improve our guess on the concentration of the acid by an iterative procedure of successive approximation. This method is full described in the solution of Problem 4 (ampholytes section).
We describe here the exact mathematical treatment to calculate the pH of weak acid (base) solutions. The understanding of this method can help in the handling of more complex problems. Consider we want calculate the H3O+ concentration of a weak acid:
| 1. AH + H2O |
In a solution of a weak acid there is another equilibrium we should consider:
| Water dissociation | ion product of water |
| 2. H2O + H2O |
Kw = [H3O+] [OH-] |
According to mass and charge conservation equations 3 and 4 must hold:
| Mass balance | Charge balance |
| 3. [Co] = [A-] + [AH] | 4. [H3O+] = [OH-] + [A-] |
By solving equation 4 for [A-] and considering that [OH-] = KW/[H3O+] (see ion product of wate) we get
![]() Kw
Kw
5. [A-] = [H3O+] - --------
![]() [H3O+]
[H3O+]
remembering that [AH] = Co - [A-] (see equ. 3), we obtain:
![]() Kw
Kw
6. [AH] = Co - [H3O+] + -------
![]() [H3O+]
[H3O+]
Eventually, by inserting expressions for [A-] and [AH] (equ. 5 and 6) into the dissociation constant of the acid, we get:
7. 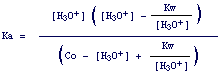
By means of this equation we can calulate the exact concentration of H3O+. However, appropiate considerations allow us to escape the use of this unpleasant cubic equation.
Normally, in an acid solution [H3O+] is more than 10-6 and thus Kw/[H3O+] = 10-14/[H3O+] < 10-8. Therefore, this term can be then neglected both at the numerator and denominator and the cubic equation reduces to:
[H3O+]2
Ka = -------------
Co - [H3O+]
which is the equation previously encountered. Furthermore, if Co >> [H3O+] we can further simplify
![]() [H3O+]2
[H3O+]2![]() [H3O+]2
[H3O+]2
Ka = ------------- = ---------
![]() Co - [H3O+]
Co - [H3O+]![]() Co
Co
This is the simplest approximate equation to solve the problem. Generally, it is preferable calculate an approximate [H3O+] by means of this last simple equation and on the basis of the result decide if the approximations are valid. Whether the result is not satisfying we will use the quadratic or the cubic equation.
Let's consider here the case of solutions containing more than one weak acid or base. This is the case, for example, of a solution containing a polyprotic acid such as carbonic acid:
| 1. H2CO3 + H2O |
|
| 2. HCO3- + H2O |
This is a more complicated case than that of a solution containing a simple weak acid and the application of the charge and material balance equations is very useful:
| Mass balances | 3. [H2CO3]i = [H2CO3]eq + [HCO3-]eq + [CO3=]eq |
| Charge balances | 4. [H3O+] = [HCO3-]eq +2[CO3=]eq + [OH-]eq |
Please note, that the coefficient of the carbonate ion is 2, in fact each ion brings two negative charges. Since the values of dissociation constant are very low we can assume that the concentration of the carbonic acid at equilibrium is equal to its initial concentration. From the expression for K1 and K2 we can obtain expressions for [HCO3-] and [CO3=] respectively:
By combining these two equations we get:
![]() [H2CO3]
[H2CO3]
7. [CO3=] = K1 K2
---------
![]() [H3O+]2
[H3O+]2
When expressions 5 and 6 are inserted into the charge balance equation (4) we have that
![]() [H2CO3]
[H2CO3]![]() [H2CO3]
[H2CO3]![]() Kw
Kw
[H3O+] = K1 -------- + 2 K1 K2
---------- + -------
![]() [H3O+]
[H3O+]![]() [H3O+]2
[H3O+]2![]() [H3O+]
[H3O+]
The equation above indicates that [H3O+] is the sum of three terms, the first and second terms correspond to [H3O+] contributed by the first and the second ionization constants respectively. From values of K1 (4.2X10-7) and K2 (4.8X10-11 ) we can expect that the second term is very small compared to the first one and thus, it should be neglected. The last term (Kw/[H3O+]) corresponds to [OH-]. In an acidic solution we can expect that this is very low and we can neglect it. Therefore,
|
[H2CO3] [H3O+] = K1 --------- [H3O+] |
[H3O+]2 = K1 [H2CO3] |
The last expression is the same we have previously deduced for a monoprotic acid.
Let's compare the effect of a tenfold dilution on the pH of the following solutions:
0.1 M HCl
0.1 M acetic acid (pK = 4.75).
|
|
|
|
|
|
|
|
|
|
|
|
The dilution of a weak acid lead to a very small increase in pH when compared to dilution of the strong acid. This is due to the fact that the dilution increases the dissociation of the weak acid (see discussion on LeChatelier principle).