The structure of the atom

Thomson with its classical experiments demonstrated (1897) that atoms contain some negative charged particles (now known as electrons). Since, normally, atoms are electrical neutral it was evident that atoms also contain positive charged particles (protons). Furtermore, according to Thomson's experiences the mass of electrons is very low and thus protons should account for most of the atomic mass. According to these observations, Thomson proposed that an atom was a uniform sphere of positive charges in which electrons are arranged in the most stable electrostatic way. It was not difficult to estimate the volume of the sphere by dividing the molar volume of a solid (cm³/mole) with the Avogadro number. The results was about 10^-24 cm³ from which a radius of 10^-8 cm can be calculated.

In 1911, after Rutheford scattering experiments, the model of Thomson was abandoned. In fact, the results obtained by Rutheford suggested that the positive charge of an atom should be concentrated in a nucleus and then an atom should not be an uniform sphere of positive charges in which electrons are arranged in the most stable electrostatic way. Therefore, Rutheford proposed a very simple model of the atom in which electrons move in elliptical orbits around a nucleus (like those of planets around sun). However this model was in conflict with physical principles known at that time. In fact, if electrons were in elliptical motion, according to the laws of electromagnetics, emission of light should be observed until the motion ceased and electrons are drawn into the nucleus. The frequency of the radiation emitted depends on the frequency of the orbital revolution, which decreases after energy is radiated, thus one should observes the emission of a continous spectra of radiations. This is in conflict with the observation that gases emitt only radiations of well defined frequencies.

Niels Bohr attempted to solve this apparent paradox by using the theory proposed by Max Planck in 1900 on the quantization of the energy. Following is a brief description of the birth of quantum theory used by Bohr to develop a new model of the atom.

Atoms are formed by electrons, protons and neutrons. The structure of an atom can be grossly represented as follows:

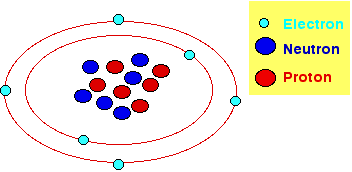Protons and neutrons form the nucleus in the center of the atom where they bound very tightly together (in the nucleus is concentrated almost all the mass of an atom.). Electrons moves around the nucleus very far from the nucleus. Electrons can leave the nucleus by an input of few energy compared to that required by neutrons and protons. Electrons and protons carry opposite electrical charges, in fact electrons and protons attract each other while electrons (neutrons) repel each other. The fact that protons bind together in the nucleus is due to a much stronger force called the strong nuclear force which has effect only under very short distances. Neutrons do not carry any charge in fact they are neither attracted to or repelled by electrons, protons and other neutrons. Normally the number of protons and electrons in an atom is the same and thus atoms are electrically uncharged. 

Atomic number. The number of protons in an atom is called atomic number and it is generally indicated with Z. Since atoms are electrically neutral Z must also correspond to the number of electrons. Thus Z indicates both the number of protons and the number of electrons. The chemical properties of an atom depend on the number of electrons forming the atom. In fact Z is unique for each atom, e.g., Z = 8 corresponds to the element oxygen, Z = 10 to argon and so forth.

The sum of neutrons and protons in an atom is called mass number and it is generally indicated with A, thus

 A = Z + N

where N is the number of neutrons.

Atoms with the same value of Z (i.e., with the same chemical properties) but with different value of A (thus, with different number of neutrons) are found in nature. These different atoms are said isotopes. For example, natural oxygen is composed by the following isotopes:

^*O¹⁴, ^*O¹⁵, O¹⁶, O¹⁷, O¹⁸, ^*O¹⁹

where the superscript is the mass number (A). The asterisk indicates those isotopes that are are unstable (radioisotopes). Radioisotopes emit energy (radioactivity) to form more stable nucleus.

The birth of quantum theory

The atom model proposed by Rutheford was in disaccord with the physics known at that time. According to laws of electromagnetism a charge in motion emits radiation until the motion stop, thus atoms should radiate light until the motion of electrons is ceased and, as consequence, electrons should be drawn into the nucleus. In other words, atoms should have been unstable. This apparent paradox was solved by Bohr's using the quantum theory of energy advanced by Planck in 1900. Before to discuss the model of Bohr, let's illustrate the principles used by Bohr in the development of its model.

Classical theory of radiation. Before 1900, according to the classical theory of radiation, it was thougt that the energy associated to an electromagnetic radiation was proportional to the the squares of the maximum amplitude of electric and magnetic fields. Altough the ondulatory theory was notably succesful to explain most optical phenomena it failed to explain the nature of the radiation of a heated solid body. In 1900 Planck solved this problem giving origin to quantum theory.

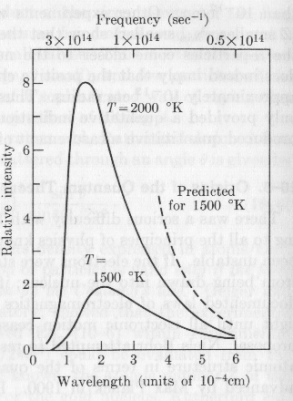The radiation of a heated solid body. It can be experimentally observed that a heated solid body emitts radiations of different frequencies. The intensity of the emission is very low at high frequencies and increases as the frequency decreases until to reach a maximum. After the maximum the intensity of emission decreases as the frequency decreases. At higher temperature, the same beahvior can be observed but i) the intensity of emission is higher at all the frequencies radiated; ii) the frequency of the radiation corresponding to the maximum intensity of emission becomes higher. These experimental observations disagrees with classical radiation theory (the distribution of radiated frequencies described by the classical theory is shown by the dashed line in the figure).

The hypothesis of Planck. The discrepancy between experimental findings and the prediction of classical radiation theory, was solved by Planck. He started with an assumption that was difficult to accept to that time (1900), i.e., a mechanical system can not assume arbitrary values of energy but only certain selected values of energy. Furthermore, he assumed that the emission of a given radiation of frequency n is due to a group of atoms oscillating at the same frequency and that the energy of this group of atoms (oscillators) is given by

E = nhn

where n is a positive integer, n the frequency and h the Planck's constant. It should be evident that since n is a positive integer the energy of the oscillator can assume only particular value which depend on n. Another assumption of Plank was that the different oscillators were in equilibrium and that their energy is distributed according to the Boltzman's. According to these hypothesis, Planck derived an expression perfectly describing the experimental distribution of radiated frequencies.

Einstein, by using the quantum hypothesis, was able to explain the temperature dependence of heat capacities of solids and the empirical laws of the photoelectric effect.

Photoelectric effect. When light collide with a metallic surface in vacuum the surface emits electrons, i.e., the energy of elecromagnetic wave is used to eiect electrons from the metal. This phenomenon is known as photoelectric effect. The classical theory of radiation was unable to explain the details of the phenomenon:

Experimental observations	Comments
1. the emission of electrons take place only when the frequency of the light is greater than a critical value (vo)	the classical theory of light affirms that the energy of the radiation is independent of its frequency and thus can not explain this observation.
2. the kinetic energy of the emitted electrons increases as the frequency increases.	Since the energy of the radiation is independent of its frequency (see above) also this observation can not be explained from the classical theory.
3. The energy of electrons do not depend from the intensity of the light but the number of emitted electrons do.	the classical theory of light affirms that the energy of the radiation is proportional to its intensity and thus we should expect that the energy of electrons depends on the light intensity.

In 1905, Einstein proposed that light consists of discrete particles (photons) of energy hn where h is the plank's constant and n the frequency of the radiation. With this assumption is quite simple to explain the photoelectric effect:

When a photon impinges on the metallic surface, part of its energy (hv) is used to extract the electron and the remaining appears as kinetic energy of the electron:

hn = w + 1/2 mv²

It should be evident that, in order to extract an electron, a photon must possess at least an energy equal to w. If w is expressed in terms of a frequency, i.e., w = hn_o the equation above becomes

hn = hn_o + 1/2 mv²

1/2 mv² = hn - hn_o

The equations above are in accord with point 1 and 2

Experimental observations	Comments
1. the emission of electrons take place only when the frequency of the light is greater than a critical value (vo)	hn = hno + 1/2 mv2 hno is the energy needed to extract the electron, if the energy of the photon is less than hno no extraction can occur.
2. the kinetic energy of the emitted electrons increases as the frequency increases.	1/2 mv2 = hn - hno when we plot kinetic energy against the frequency of the radiation we obtain a straight line with slope h and intercept hno as experimentally found.

Finally, point 3 can be explained by assuming that light intensity is associated with the number of photons arriving on the metals and thus more electrons can be extracted.