DT = K ----------------------------
The Raoult's law states that the vapor pressure exerted by a liquid depends on its mole fraction and is expressed by
| 1. P = xPo |
where x = mole fraction of the liquid Po = vapor pressure of pure liquid P = vapor pressure after the addition of a solute to the liquid. |
Remembering that the mole fraction of the liquid is moles of liquid/total moles it should be evident that the increase of the total moles, by adding a solute, will result in a decrease of x and as consequence the vapor pressure of the liquid will decrease. This phenomenon is known as vapor pressure lowering.
The variation of vapor pressure, after the addition of a solute is given by
| 2. DP = Po - P |
where Po = vapor pressure of pure liquid P = vapor pressure after the addition of a solute. |
According to Raoult's law (P = xPo) P can be substituted with xPo and thus
3. DP = Po - xPo = Po (1 - x)
For a solution with two components 1 - x = xs (the mole fraction of solute) and then equ 3 can be written as
4. DP = xsPo
Therefore, the vapor pressure lowering is directly proportional to the mole fraction of solute.
Colligative properties. It should be noted that the vapor pressure lowering, depends only on the concentration of solutes but not on their nature. Properties of solutions that depends only on solute concentration and not on the nature of the solute are said colligative properties.
Ideal solutions. As in the case of gas, the study of solutions can be greatly simplified by considering an ideal solution and then extending the results to real solutions. For a mixture of ideal gases, since there is no interactions between molecules, the properties of each gas does not change upon mixing. As an example, according to Dalton's law, the total pressure of the mixture is the sum of partial pressure of each gas in the mixture as well as the total volume is the sum of partial volume of each gas in the mixture. Altough liquids exist for the existence of interaction between molecules, for many liquid diluted solutions we can reasonably assume that there are no interactions between molecules thus having an ideal solution. An ideal solution is defined as the one as one which obey the Raoult's law or, equivalently, which can be formed from its components with no evolution or absorption of heat.
The Raoult's law explains the common observation that when we add some salt to water, the boiling point of water increases. In fact the boiling point is inversely related to the vapor pressure, i.e., the lower the vapor pressure the higher the boiling point. According to Raoult's law, the vapor pressure decreases upon the addition of a solute and thus the boiling point of water increases upon the addition of a solute. Since the decrease of the vapor pressure of solvent is proportional to the mole fraction of solute, the increase of boiling temperature of solvent should be also proportional to the molar fraction of solute. It can be demonstrated that the variation of temperature is given by
|
DT = K xsolute
|
where K = constant characteristic of a given solvent xsolute = mole fraction of solute. |
By remembering the definition of mole fraction, we have
![]() molessolute
molessolute
DT = K ----------------------------
![]() molessolute
+ molessolvent
molessolute
+ molessolvent
Assuming that, for a diluted solution, molessolvent >> molessolute we can write
![]() molessolute
molessolute
DT = K -------------
![]() molessolvent
molessolvent
and expressing moles of solvent as grams/mw we get
![]() molessolute
molessolute
DT = K mwsolvent --------------
![]() gramssolvent
gramssolvent
Eventually, by multiplying and dividing with 1000, we have that
![]() (K mwsolvent)
(K mwsolvent)![]() molessolute
molessolute
DT = ------------- ---------------- 1000
![]() 1000
1000![]() grams
solvent
grams
solvent
and indicating with Kb the first term (K mwsolvent/ 1000) and remembering that the second term is the molality (m) of the solution, we can write
DT = Kb m
Therefore the boiling point elevation is directly proportional to the molality of the solution.
The addition of a solute to a solvent produces another effect known as freezing point lowering. When a solute is added to a solvent the freezing point decreases and it can be demonstrated, analogously to the boiling point elevation, that DT = Kf m, i.e., the decrease in the freezing point is directly proportional to the molality of the solution.
Ionics vs. covalent substances. As previously stated, the vapor pressure lowering is a colligative property, i.e. it depends on the number of molecules (ions) in the solution.
When we dissolve an electrolyte in water this dissociates giving rise to more than one chemical species and this must be taken in account to calculate the molality of the solution.
For example, if 1 mole of NaCl is dissolved in 1000 gm of water we obtain a solution which is 1 molal in Na+ and 1 molal in Cl - thus, the total molality of the solution is 2 m. In fact, it can be observed that such solution produce a freezing point depression of 2Kf.
When we deal with nonideal solutions there is a noticeable deviation from the laws deduced above. For example, the experimental freezing point depression may differ from that calculated (DT = Kf m). Since Kf is a constant we can imagine that the effective concentration of the solute differs, due to molecules interaction, from that calculated. This effective concentration is known as activity.
Activity can be determined by comparing the expected value of DT with that experimentally determined:
|
|
|
|
|
|
By dividing the two equation above we have
![]() DT
DT![]() Kf
m
Kf
m![]() m
m
![]() --- = --------------
= ------------
--- = --------------
= ------------
![]() DT1
DT1![]() Kf
(activity)
Kf
(activity)![]() (activity)
(activity)
Since m is known, DT can be calculated and DT1 can be experimentally determined then we can determine the activity.
In a ideal solution containing two volatile compounds, both components will follow the Raoult's law and we can write:
| 1. P1 = x1 Po1 | 2. P2 = x2 Po2 | 3. PT = P1 + P2 = x1 P o1 + x2 Po2 |
where
P1 and P2 = actual vapor pressure exerted by component 1 and 2 respectively;
Po1 and Po2 = vapor pressure of pure component 1 and 2 respectively;
x1 and x2 = mole fractions of component 1 and 2 respectively.
PT = total pressure exerted by the two components
Let's consider a solution of benzene (Po1 = 75 mm Hg ) and toluene (Po2 = 22 mm Hg ) having the following composition:
|
x1 (benzene) = 0.33
|
x2 (toluene) = 0.67
|
The partial vapor pressure of the two components is
|
Benzene
|
Toluene
|
|
P1 = 0.33 X 75 mm Hg = 25 mm Hg
|
P2 = 0.67 X 22 mm Hg = 14 mm Hg
|
and the total pressure exerted by vapors is PT = P1 + P2 = 39 mm.
From the Dalton's law we know that P = Pt xa , where
P = pressure exerted by a component in the vapor mixture.x = the molar fraction (in the vapor) of the component considered.
Pt = the total pressure exerted by the vapor mixture.
Therefore, we can calculate the composition of the vapor:
|
|
|
|
|
|
In the following figure is shown the dependence of the partial and total vapor pressure of the solution on concentration (mole fraction).

Let's compare now the composition of the solution described above with the composition of its vapor:
|
|
|
|
Toluene = 67% |
Toluene = 36% |
As can be observed the composition of the vapor is very different from that of the starting solution. In fact, the vapor is about twice as rich in benzene as the liquid. It is worth noting that the vapor results enriched of the more volatile component (benzene). If the vapor is collected and condensed we will get a solution which is more rich in benzene. The reiteration of the condensation-evaporation process (distillation) will produce a vapor that is nearly pure benzene and a liquid that is nearly pure toluene. The process of distillation can be well illustrated by plotting the boiling point of a solution versus the composition of the solution and the composition of the vapor.
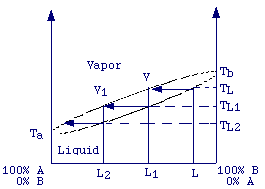 Suppose
that the initial solution of components A and B boils at temperature
TL , there will be the production of a vapor with composition
V which is enriched in the more volatile component (A ). If this
vapor is collected (removed from the system) and condensated it will produce
a liquid of a composition L1 (=V) which boils at temperature
TL1 and giving raise to a vapor still richer in A.
From the figure it should be evident that the repetition of the evaporation-condensation
process tends to produce a vapor (upper line) nearly 100% A.
Suppose
that the initial solution of components A and B boils at temperature
TL , there will be the production of a vapor with composition
V which is enriched in the more volatile component (A ). If this
vapor is collected (removed from the system) and condensated it will produce
a liquid of a composition L1 (=V) which boils at temperature
TL1 and giving raise to a vapor still richer in A.
From the figure it should be evident that the repetition of the evaporation-condensation
process tends to produce a vapor (upper line) nearly 100% A.
On the other hand, once the vapor obtained is removed from the system we obtain a liquid which is richer in the less volatile component (B). The remotion of vapor will lead to a new equilibium at higher temperature producing a liquid still richer in the less volatile component (B). Repetition of this process tends to produce a liquid which is 100% B.
This is not always true for non-ideal solutions. For non-ideal solutions we can have, depending on the system analysed and on the molar fractions of the liquid components, a vapor enrinched in the less volatile component or a vapor having the same composition as the liquid. Eventually, let's remember that some solutions upon distillation give rise to a vapor having the same composition as the liquid. These solutions are called azeotropes.
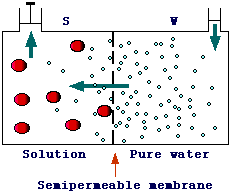 Osmosis is a phenomenon occuring when two solutions having different concentrations
are separated by a semipermeable membrane. A semipermeable membrane is one that
is permeable to the solvent (water), but not the solute. Actually, a true semipermeable
membrane does not exist but there are many membranes (e.g., some animal proteinic
membranes) that allows only small molecules to pass through. Let's consider
a system, such the one in figure, in which pure water (W) and a solution
(S, e.g., water and sugar) are separated by a semipermeable membrane.
Only water can pass the membrane.
Osmosis is a phenomenon occuring when two solutions having different concentrations
are separated by a semipermeable membrane. A semipermeable membrane is one that
is permeable to the solvent (water), but not the solute. Actually, a true semipermeable
membrane does not exist but there are many membranes (e.g., some animal proteinic
membranes) that allows only small molecules to pass through. Let's consider
a system, such the one in figure, in which pure water (W) and a solution
(S, e.g., water and sugar) are separated by a semipermeable membrane.
Only water can pass the membrane.
In this system, a net flow of water from section W to section S can be observed (as indicated by the increase of water level in S and the decrease in W). This difference in water level will produce a difference in pression (pS > pW) opposing the water diffusion from W to S. When this pression counters exactly the diffusion process an equilibrium is reached and no net flow of water is observed. The pression at equilibrium is known as osmotic pressure (p). It can be demonstrated (see thermodynamics) that, with some approximation:
|
|
|
where M is the molarity of the solution. Remembering that moles = grams/molecular weight it results that the smaller the molecular weight the higher the osmotic pressure.
Donnan effect. The molecular weight of hydrophylic colloidal particles (e.g., proteins) obtained by osmotic pressure measurements is always lower than that determined by other methods. This can be explained by the so called Donnan effect which is due to the fact that proteins are multicharged molecules (polyelectrolytes) and its charges are neutralised by the presence of small ions (counterions). Although, the membrane is permeable to counterions they cannot cross the membrane for the electrostatic forces holding togheter protein and counterions. Thus, the osmotic pressure measured is due both to protein and counterions and the molecular weight calculated is the average of that of protein and severals small ions.
Cells and osmotic pressure. Solutions having the same osmotic pressure of cells (i.e. the concentration is the same on both sides of the cellular membrane) are said isotonic. Solutions having a concentration lower than that in cell are said hypotonic. When a cell is an hypotonic solution, water is drawn into the cell thus leading to its swelling and rupture. Finally, hypertonic are those solutions having a concentration higher than that in cell. When a cell is an hypertonic solution, water is drawn out of the cell thus leading to its collapse.