Let's consider two bodies at different temperatures (Ta and Tb)
separated by a conductive medium, if Ta > Tb
then there will be a transfer of heat from A to B until a thermal equilibrium
is reached. Let's imagine that at the time t an amount of heat
q is transferred from A to B with a consequent change of Ta
and Tb, we can write:
Qta = Qa - q
Qtb = Qb + q
|
where Qa and Qb are the initial
heat content of A and B respectively, and Qta and Qtb
are the heat of A and B at the time t. |
If at the same time t, the same amount of heat is added to A and removed
from B, we have
Qta = Qa - q + q = Qa
Qtb = Qb + q - q = Qb
Therefore, in this process, the heat content and the temperature of A and B
remain unchanged. For an external observer, since there is no change in the
temperature of A and B, the system appears to be in "equilibrium". This apparent
equilibrium, obtained by adding and removing heat at the same rate, is referred
to as steady-state. Let's consider another different example, the transformation
of a product A to a product B by means of an hypothetical device:
Input
==============>
A
|
System
transformation occurs here.
|
Output
=============>
B
|
If we continuously remove B from system (i.e., B does not accumulate
in the system) and continuously add A to the system we
realize a steady state process.
Driving
forces and resistances
|
It has been shown by Fourier that the rate of heat transfer between two bodies
at differents temperatures can be calculated as follows:
 A A
q = k ----Dt
 Dx Dx |
where
q = heat flow rate in J/s (W, watts)
A = the area perpendicular to the flow in m2
Dt = the temperature gradient (oK
or oC)
Dx = the distance between the two area
at different temperatures (m)
k = the thermal conductivity i.e., the heat flow rate when A,
Dt and Dx
are unitary which depends on the material forming the system.
|
The difference of temperatures (Dt) is known
as the driving force of the process. In fact if no temperature difference
exists no exchange of heat is possible.
Many processes involve the flow of a quantity under the action of a driving
force or potential, for examples:
|
Flow
|
driving force (potential)
|
| fluids |
gradient of pressure |
| electricty |
electric potential difference |
| heat |
gradient of temperature |
From the equation of Fourier, results that the rate of heat transfer is directly
proportional to Dt (the driving
force) and directly proportional to kA/Dx.
This last term depends on the particular system we are analyzing and thus it
is a measure of the ability of a given system to transfer heat. Of
course its inverse Dx/kA is a measure
of the resistance offered by the system to the heat transfer. Indicating
with R (thermal resistance) the term Dx/Ka, the Fourier's
law can be rewritten as
q = Dt/R
In general, processes involving the flow of a quantity under the action of
a driving force or potential can be written as the ratio of the driving
force with a resistance. For example, equ 2 is identical to the expression
of Ohms' law (I = DV/R) which describes
the flow of electrical charges under the action of a potential difference.
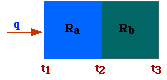 Serie.
In fig are represented two resistance in serie. Under steady-state conditions,
the heat (or other) entering the resistances must equals the
heat leaving them. This implies that the flow of heat through
Ra must match the flow of heat through Rb, thus
Serie.
In fig are represented two resistance in serie. Under steady-state conditions,
the heat (or other) entering the resistances must equals the
heat leaving them. This implies that the flow of heat through
Ra must match the flow of heat through Rb, thus
by adding the last two expressions above and solving for q we get
Therefore, the total resistance (Rt), for an arrangement in series,
is the sum of the single resistances.
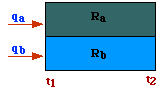 Parallel.
In this case (see fig), under steady-state conditions, the heat leaving the
resistances must be the sum of heat entering the single resistances:
Parallel.
In this case (see fig), under steady-state conditions, the heat leaving the
resistances must be the sum of heat entering the single resistances:
 DT DT DT DT
qt = qa + qb = -------- + ------
 Ra Ra Rb Rb
|
 1 1 1 1
qt = DT (---- + -------)
 Ra Ra Rb Rb
|
 Serie.
In fig are represented two resistance in serie. Under steady-state conditions,
the heat (or other) entering the resistances must equals the
heat leaving them. This implies that the flow of heat through
Ra must match the flow of heat through Rb, thus
Serie.
In fig are represented two resistance in serie. Under steady-state conditions,
the heat (or other) entering the resistances must equals the
heat leaving them. This implies that the flow of heat through
Ra must match the flow of heat through Rb, thus Parallel.
In this case (see fig), under steady-state conditions, the heat leaving the
resistances must be the sum of heat entering the single resistances:
Parallel.
In this case (see fig), under steady-state conditions, the heat leaving the
resistances must be the sum of heat entering the single resistances: