Laws of thermodynamics

The first law

The first law of thermodynamics is the law of the conservation of energy and can be stated as follows:

the change in energy of a system must match the amount of heat and work exchanged with the surrounding in such a way the energy of the universe results unchanged.

In mathematical terms it can be expressed by equ. 1 or equ. 2.

1. DE = Q - W
2. DE = Q + W

These two apparently differents expressions arise from differents convention on the sign attributed to the work.

The first law was developed during studies on steam engines in which the heat added to the system is partially transformed in work and thus work made by system was considered positive (of course work made on the system is negative). In this case, the first law is expressed by equ. 1 and can be stated as follows:

the total change in energy of a closed system is equal to the heat added to the system minus the work done by the system.

Another convention consider negative the work made by system and positive the work made on the system and the second law is expressed by equ. 2.

Confusion about the sign of work can be avoided by realizing that work made on the system must increase the energy of the system and work made by the system must decrease the energy of the system. Eventually, let's say that heat evolved by system is always considered negative (the energy of system decreases) while heat absorbed by system is always considered positive (the energy of system increases).

Since the first law will be used to derive many important equations describing the behavior of thermodynamic systems, it is worth realize that the two equations above are perfectly equivalents.

In order to clarify this point, let's consider a system (a gas) which exchanges PV work with its surrounding (please note that for the moment we limit our discussion to systems which can accomplish only PV work). When we compress the gas (work is done on the system) from Vi (initial volume) to Vf (final volume) it results

3. W = P (Vf - Vi) < 0 (in fact, Vf < Vi)

In the case we consider positive the work done on the system, equ. 2 (DE = Q + W ) will hold and we must change the sign of the work, i.e., W = -PDV. Therefore, the first law will given by Equ. 4

4. DE = Q + W = Q + (- PDV) = Q - PDV

On the other hand, if we we consider negative the work done on the system equ. 1 (DE = Q - W) will hold and there is no need to change the sign of the work, i.e., W = PDV. Therefore, the first law will be given by Equ. 5

5. W = Q - PDV

It is evident that independently from the convention used we obtain the same equation. It is not difficult to prove that in the case of an expansion of the gas the same equation holds. Therefore, independently from the convention used, the first law, in the case of PV work, can be written as

6. W = Q - PDV

Internal energy

We have seen that the variation of the energy of a system can be expressed in term of internal, kinetic and potential energy (see equ.7) and thus the first law can be written as in 8.

7. DE = DU + DEp + DEk
8. DE = DU + DEp + DEk = Q + W

However, if the process considered (e.g., a chemical reaction) does not involve variations of position and velocity of the system, DEp and DEk will be zero and only the internal energy of the system will be affected by the process. Thus the first law reduces to equ. 9.

9. DU = Q + W

Friction

Normally, when works is performed, friction (f) exists and additional work must be done to overcome it and the first law can be written as in 10. Since f can be thought as an additional amount of heat to add to the system or dissipated by the system, Q and f are grouped together and thus we get 11.

10. DU = Q + f + W

11. DU  = Q + f + W = Q + W

Volume/Pressure constant processes

Volume constant processes

Let's consider a process (e.g., a chemical reaction), which is run in a close wessel. Since the volume is constant no PV work can be accomplished. Therefore, if our system can not accomplish any other kind of work (e.g, electric work), the first law (equ. 1) reduces to equ. 2

1. DU = Q - PDV

 2. Q = DU

In other words, the heat exchanged by a system at constant volume, corresponds to the variation of the internal energy of the system. Since U is a function of state, in a constant volume process Q is a function of state. Therefore in order to measure the variation of internal energy of a system we just need to measure the amount of heat exchanged.

For a chemical reaction DU allows to have information on the stability of reactants and products. If heat is evolved Q is negative (DU < 0) and thus the internal energy of products is lower than that of reactants (exotermic reactions). The opposite will be true if Q is positive, i.e., the internal energy of products is greater than that of reactants (endothermic reactions).

Pressure constant processes

In a constant pressure process, the first law (equ. 1) can be rearranged as in equ. 3 and by indicating with H the term U + PV we have equ. 4.

1. DU = Q - PDV

3. Q = DU + PDV = (Uf - Ui) + P(Vf - Vi)

Q = (Uf + Ui) + (PVf - PVi)
Q = (Uf + PVf) - (Ui + PVi)

 4. Q = Hf - Hi = DH

Since U and PV are functions of state, H is a function of state too and it is known as enthalpy. By summarizing, at constant pressure, the heat exchanged by a system corresponds to the variation of its enthalpy (a function of state) and thus Q is a function of state (at constant pressure). For exotermic reactions is DH < 0 while for endothermic reactions DH > 0. Enthalpy, because constant pressure processes are very common, is also called heat content.

By comparing the expressions of first law obtained in a volume and in a pressure constant process respectively,

2. Q = DU 3. Q = DU + PDV

we can see that the difference between DH and DE is the term PV, for reactions involving only liquids and solids the variation in volume is very small and if the pressure at which the reaction is run is relatively low (e.g., 1 atm), the term PDV can be neglected and thus DH @ DU. Instead, for a gas the variation in volume can not be neglected and according to the equation of ideal gas (equ. 5) we have equ 6.

5. PV = nRT 6. DH = DU + DnRT

Specific heat

In the SI system specific heat (heat capacity) is defined as the amount of energy (Joule, J) needed to raise 1 Kg of material one degree celsius.

From the discussion above we know that the amount of heat exchanged by a system depends on how the process is performed (i.e., Q is not  a function of state). Therefore, also the specific heat depends on how the heat is absorbed by the system.

In a constant volume process, since DU = Q, the specific heat is defined as the variation of internal energy of a system with respect to temperature (equ. 7). Analogously, in a constant pressure process, the specific heat, is defined as in 8.

7. Cv = dU/dT  ==> dU = dQ = CvdT 8. Cp = dH/dT ==> dH = dQ = CpdT

Both the values of Cp and Cv depends on temperature and thus also the variation of enthalpy and internal energy depends on temperature. In order to integrate the equation above, to obtain the values of DH and DU,  we need to know how the specific heat depends on temperature. When the range of temperature considered is small, specific heats can be considered constant and equs. 9 and 10 hold.

9. DH = CpDT

10. DU = Cv DT

Finally, according to equ. 6 we get equ. 11.

6. DH = DU + DnRT 11. Cp = Cv + nR

For liquid and solids only a small difference exists between Cp and Cv thus Cp@ Cv

Isotherm processes

According to kinetic theory of gases the internal energy of an ideal gas depends only on the temperature. Therefore, in an isotherm process (constant temperature process), since DU = 0 then the first law (equ. 1) reduces to equ. 2.

1. DU = Q - PDV 2. Q = PDV

This last equation, since P is not constant, is best written as in 3 and remembering that P = nRT/V we get 4 which integrated gives 5.

3. Q = PdV 4. Q = nRT dV/V = nRTdV/V 5. Q = nRTdV/V = nRT ln V2/V1

According to Boyle's law, equ. 6 also holds.

Boyle's law

P1V1 = P2V2 V2/V1 = P1/P2

 

 6. Q = nRTdV/V = nRT ln P1/P2

By summarizing, for an isotherm process we have that

Q = nRTdV/V = nRT ln V2/V1

 6. Q = nRTdV/V = nRT ln P1/P2

 

Adiabatic processes

An adiabatic process is the one in which the system can not exchange heat with the surroundings. In such conditions, considering an infinitesimal process, the first law (equ. 1) reduces to equ 7.

1. dU = Q - PdV 7. dU = -PdV

Remembering that dU = CvdT and P = nRT/V we get 8 and by dividing with T we get equ. 9

8. CvdT = -PdV ==> CvdT + PdV = 0

==> CvdT + nRT (dV/V) = 0

 9. Cv(dT/T) + nR(dV/V) = 0

The integration of equ. 9 (assuming that Cv is constant) gives equ. 10.

10. Cv ln(T2/T1) + nR ln(V2/V1) = 0

Remembering that nR = Cp-Cv and by dividing by Cv we obtain 11 and 12.

11. Cv ln(T2/T1)+ Cp-Cv ln(V2/V1) = 0

 12. ln(T2/T1) + (Cp-Cv)/Cv ln(V2/V1) = 0

By posing g = Cp/Cv, the term (Cp-Cv)/Cv becomes g - 1 and thus we get 13. By eliminating logarithms we obtain equs. 14 and 15.

13. ln(T2/T1) + g - 1 ln(V2/V1) = 0

14. T2/T1 + (V2/V1)g - 1 = 0 15. T1/T2 = (V2/V1)g - 1

Since, for an ideal gas, T1 = P1V1 and T2 = P2V2, it results that for an adiabatic process

P1V1(V1g - 1) = P2V2(V2g - 1)

P1V1g = P2V2g

 

Standard enthalpy changes

Enthalpy of reactions is normally given as standard enthalpy change, i.e. when both reactants and products are at 298 oK and 1 atmosphere and is indicated as DHo. As an example, equ. 1 indicates that when one 1 mole of C reacts with O2 and is completely converted in CO2, at 298 oK and 1 atmosphere, 94.05 kcal are developed.

1. C + O2 = CO2, DHO = -94.05 kcal

Bomb calorimeter

The heat evolved by a combustion reaction can be measured by means of the so called bomb calorimeter:

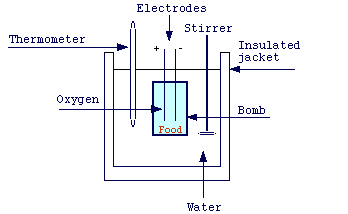
The combustion of the sample leads to an increase in the temperature of a known weight of water. Since one Kcal is the amount of energy (heat) required to raise the temperature of 1.0 kg of water by 1 degree, the heat evolved by combustion is easily calculated. However, for some reactions, this experimental determination is difficult to accomplish.

Let's consider in more detail the reaction of combustion of carbon (equ. 1), if a large excess of O2 is used we are quite sure to convert all C into CO2 and we can measure the DH. This is not true for the reaction of partial combustion (equ. 2), in fact in order to convert all C into CO, an excess of O2 must be used but in this condition part of CO can be oxidized to CO2.

1. C + O2 = CO2, DHO = -94.05 kcal 2. C + 1/2 O2 = CO, DHO = ?

Hess law

The fact that enthalpy is a function of state helps us to calculate the DH of reaction 2. The reaction of complete combustion of C (equ. 1) can be thougt as the sum of reactions 2 and 3, in fact by summing these two equations (and by eliminating terms found on both side of the chemical equation) we get equ 1.

2. C + 1/2 O2 = CO, DHO = ?

3. CO + 1/2 O2 = CO2 , DHO = -67.63 kcal

1. C + O2 = CO2, DHO = -94.05 kcal

Since enthalpy is a function of state, the enthalpy of this last reaction must be the sum of enthalpy of reaction 2 and 3 and this allows to calculate enthalpy of reaction 2 (see 4 and 5).

4. DH1 = DH2 + DH3

5. DH2 =  DH3 - DH1 = -94.05 + 67.63 = -26.42 kcal

This is an application of Hess' law of constant heat summation which states that the heat evolved or absorbed at constant P is the same regardless of the paths followed. Therefore, reactions can be algebraically combined (as made above) to obtain the desired reaction and the corresponding value of enthalpy.

Enthalpy of formation

Enthalpy of formation represents the variation of enthalpy (at standard conditions) occuring when a compound is formed by its elements, as an example:

C + 1/2O2 = CO
DH0 = HCO - HC - HO2

The enthalpy of formation of elements is zero by definition and thus DH0 = HCO = - 67.6 kcal. The enthalpy of formation of several compound has been measured and tabulated. From this tabulated values, by means of Hess' law, it is possible to compute the variation of enthalpy for many other reactions (see problems).

Temperature dependence of enthalpy

The DH of chemical reactions depends on temperature, here we will develop an expression for the temperature dependence of DH.  Let's consider the generic reaction aA + bB = cC + dD for which DH1, the enthalpy change at temperature T1, is known. Our goal is to relate DH1 to DH2, the enthalpy change at temperature T2. Let's  imagine to accomplish the trasformation of reactants in products, at temperature T1, in the following way:

1. The temperature of reactants is changed from T1 to T2, the enthalpy change associated with this process is indicated as DH'.

2. The reactants are then transformed in products at temperature T2 (DH2)

3. The temperature of products is then changed from T2 to T1 (DH").

The result of the steps above is the trasformation of reactants in products at temperature T1 for which the enthalpy change is DH1. Since enthalpy is a function of state, it should be evident that:

DH1 = DH' + DH2 + DH"
DH2 = DH1 - DH' - DH"

DH' and DH" can be easily calculated if the specific heat of reactants and products are known:
 
DH' = Cpreactants (T2 - T1)
DH" = Cpproducts (T1 - T2)

thus DH2 = DH1 - Cpreac (T2 - T1) - Cpprod (T1 - T2).

If in the second term on the right-hand side of the equation we exchange T2 with T1 we can write:

DH2 = DH1 + [Cpreac(T1 - T2) - Cpprod (T1 - T2)]

DH2 = DH1 + DCp(T1 - T2)

Therefore the difference in DH depends on the difference of the specific heat of products and reactants. It is worth noting that the expression above is valid if specific heats do not change with temperature or if the variation with temperature is the same for reactants and products. If this assumption does not hold, we should consider the integral of (DCpdt).