 To conclude
this section, let's make some considerations on the meaning of the words reversible
and equilibrium using a constant P and T process as an example. Consider, three
differents states for a system:
To conclude
this section, let's make some considerations on the meaning of the words reversible
and equilibrium using a constant P and T process as an example. Consider, three
differents states for a system:
Here we will introduce two important thermodynamics functions, the Helmholtz free energy (F, work function) and Gibbs free energy (G). The importance of these two functions can be summarized as follows:
1] G (at constant T and P) and F (at constant V and T) represent the maximum work we can obtain from a given process.
2] G and F allows to predict the evolution of a system between
different states. Consider two different states (A and B) of a system for which
we can calculate F and G. We will show that when
|
Gb - Ga or Fb -
Fa < 0
|
the system in state A can spontaneously reach state B thus producing work. |
|
Gb - Ga or Fb -
Fa > 0
|
the system in state A can not spontaneously reach state B. |
|
Gb - Ga or Fb -
Fa = 0
|
state A is in equilibrium with state B. |
From the second law we know that equations 1-3 hold for a reversible process, while equations 4-6 hold for an irreversible process.
|
Reversible |
|
| 1. dS = dQ / T 2. TdS = dQ 3. TdS - dQ = 0 |
4. dS > dQirr
/ T 5. TdS > dQirr 6. TdS - dQirr > 0 |
It should be evident that the positive difference TdS - dQirr (equ. 6) indicates the heat dissipated under an irreversible process. By indicating with dq this difference and by dividing with T we obtain we have
|
7. TdS = dQirr + dq
|
8. dS = (dQirr /T) +
dq/T
|
The term dq/T in 8, represents the increase of entropy generated during an irreversible process and here indicated as Sg (see 9 and 10).
| 9. dS = (dQirr /T) + dSg | 10. TdS = dQirr + TdSg |
By inserting equ. 10 in the expression of the first law (dE = dQ - dW, were W includes all possible works the system can accomplish) we get equ. 11-13 (reversible process) annd 14-15 (irreversible process).
|
Reversible |
|
|
11. TdSg =
0; dQ = TdS |
14. TdSg
> 0; dQirr = TdS - TdSg
15. dE = (TdS - TdSg) - dWirr 16. dE - TdS = - dWirr - TdSg |
If we consider an isothermal process the term dE - TdS is the total differential of E - TS in fact:
d(E - TS) = dE - TdS - SdT = dE - TdS (at constant T)
This new function of state (E, T, S are functions of state) is known as work function or Helmholtz free energy and here indicated with F. Accordingly, the equations above can rewritten as in 17 and 18.
|
|
|
|
|
|
Let's consider an isothermal process in which a system goes from the state A to the state B through a reversible and irreversible path. Since F is a function of state, its variation will be the same in both processes. And thus equ. 19-21 will hold.
| 19. dF = - dWrev = - dWirr- TdSg | 20. dWrev = dWirr + TdSg | 21. dWrev > dWirr |
Taking as an example, the expansion and the compression of a gas the fact that Wrev > Wirr leads to the following conclusions:
1] during a reversible expansion we get more work than during an irreversible one.
2] a reversible compression requires less work than that required for the irreversible compression.
Therefore, because of irreversibility, we get less work during the expansion of a gas and we need more work for its compression.
From the definition of F we can deduce the existence of another important function of state. In fact considering that dW includes all the possible kinds of work and then also PV work we can write:
dE - TdS = - dWnet - PdV
from which
dE + PdV - TdS = - dWnet
The term dE + PdV is the total differential of H (for a constant P process) and thus:
dH - TdS = - dWnet
This new function of state is the Gibbs free energy (here indicated with G) and it represents all works other than PdV work (Wnet). By summarizing
G = H - TS = E - TS + PV = F + PV
According to the principle of increase of entropy, for any system evolving from a state A to a state B equ. 1 must hold:
1. dSnet = dSsys + dSsurr > = 0
In this equation, the inequality holds for irreversibles (spontaneous) processes and the equality holds for reversibles processes.
When dSnet < 0 the system can reach state B only with an external intervention (i.e., an input of energy). In other words state B can spontaneously reach state A and not viceversa.
Therefore, in order to establish if a given process (e.g. a chemical reaction) can occur spontaneously we need to calculate the variation of entropy of system and surroundings. A more convenient way to establish the spontaneity of a process should be one depending only on the properties of the system.
In the following discussion we will take a chemical reaction as an example but all the principles derived here apply to any thermodynamics process (e.g. phase changes). We know that chemical reactions can be exothermic (they transfer heat to surroundings) or endothermic (they absorb heat from surroundings) thus if we know the amount of heat exhanged during the reaction we can calculate the variation of entropy of surroundings. Of course, the variation of entropy of the surrounding will have an opposite sign of the variation of entropy of the system. Therefore, the principle of increase of entropy can be written as in 2
| 2. dSnet = dSsys - (dq/T)sys > = 0 | 3. dSnet = dS - dq/T > = 0 |
In this form dSnet depends only on the properties of the system and we can eliminate the subscripts as in 3.
By multiplying with T and changing the sign of all terms we obtain 4 and 5.
| 4. TdSnet = TdS - dq > = 0 | 5. -TdSnet = dq - TdS < = 0 |
If the reaction is run at constant V , dq = dE and thus equ. 6 holds. By indicating -TdSnet with dF we get 7, i.e., the work function defined above.
| 6. -TdSnet = dE - TdS < = 0 | 7. dF = dE - TdS |
It should be evident that for a reaction run at constant P (the most common case), dq = dH and 8 and 9 will hold.
| 8. -TdSnet = dH - TdS < = 0 | 9. dG = dH - TdS |
Eventually it should be noted that, due to the change of sign, G and F decrease when the process is spontaneous and of course increases for non spontaneous processes. At equilibrium dG = 0 and dF = 0.
We have previously remarked that an equilibrium state is a compromise between the tendency of systems to reach a state of minimum energy and the tendency of systems to reach a state of maximum entropy (disorder). This can now well illustrated by applying the function of Gibbs to some hypothetical reactions run at constant P (for constant volume we should use the function of Helmholtz)
Case 1. The entropy of system decreases and the energy of system decreases, e.g., TdS = -10, dH = -20 (exothermic reaction).
dG = -20 -(-10) = -10
A reaction in which the entropy of products is less than that of reagents (dS<0) can proceed only if the reaction evolves heat (exothermic) in a sufficient amount to give dG<0.
Case 2. The entropy of system increases and the energy of system increases, e.g., TdS = +10, dH = +5.
dG = 5 -(-10) = -5
A reaction in which the energy of products is greater then that of reactants (dH>0) can proceed only when the increase in entropy is large enough to give dG<0.
Case 3. The entropy of system increases and the energy of system decreases, e.g., TdS = +10, dH = -5.
dG = -5 - 10 = -15
In this case no conflict exists between entropy and enthalpy. Any value of dH and dS will result in a negative value of dG.
It is worth noting that in cases 1 and 2 there will be an equilibrium between products and reagents. In fact, in these cases one driving force favours the formation of products and the other one favours the formation of reagents, at equilibrium we will found both reagents and products. In case 3, instead, both enthalpy and entropy favours the formation of product and no equilibrium exists, at equilibrium we will found only the products.
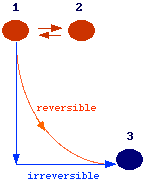
 To conclude
this section, let's make some considerations on the meaning of the words reversible
and equilibrium using a constant P and T process as an example. Consider, three
differents states for a system:
To conclude
this section, let's make some considerations on the meaning of the words reversible
and equilibrium using a constant P and T process as an example. Consider, three
differents states for a system:
States 1-2 are in equilibrium (thus dG = 0).
States 1-3 are not in equilibrium and the system in state 1 can reach spontaneously state 3 via a reversible or irreversible path. We have defined a reversible path as the one made up by a succesion of quasistatic process, i.e., a succesion of equilibrium states. This means that for each successive points on the reversible path dG =0. Therefore the condition dG = 0 defines both a condition of equilibrium and a condition of reversibility. But, if we calculate the finite variation of G between state 1 and 3 we have DG <O while for state 1 and 2 we have DG = 0.