Gases

Starting from 1660, some simple laws describing the behavior of gases were experimentally determined. Such laws can be mathematically deduced (kinetic theory of gases) assuming that

1. The volume occupied by molecules is negligible when compared to the volume occupied by the gas. Therefore the volume occupied by the gas is the volume really available to gas molecules for their movements. 

2. There is no interactions between molecules (except for brief moments).

The laws which can be deduced, when the assumptions above hold (generally for gases at low values of pressure), are known as laws of ideal gases.

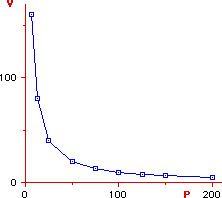
Boyle's law

Boyle's law states that at constant temperature (isothermal process) the volume of a gas is inversely proportional to its pressure. In other words, an increase of pressure leads to a decrease of the volume of a gas and viceversa. In mathematical terms the law of Boyle can be expressed by the following equation PV = const (at constant T) which is the equation of an hyperbola (see fig). If the plotting of P vs V yields an hyperbola than we can affirm that the gas is ideal otherwise the gas is nonideal (imperfect) at the given temperature. The plot can be made at different temperatures thus obtaining a family of curves called isotherms. If all curves are hyperbolas the gas obeys Boyle's law at the given temperatures.

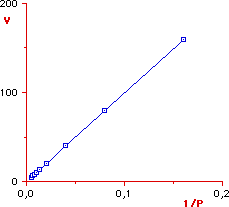
Since deviations from a straight line can be more easily detected, it is very useful to transform the equation of Boyle in such a way to obtain the equation of a straight line. The Boyle's equation can be solved for V thus obtaining 1 V = const --- P By plotting V versus 1/P (or P versus 1/V), we obtain a straight line with slope = const. Therefore, a gas is ideal when the plot of V versus 1/P (or P versus 1/V) yields a straight line.

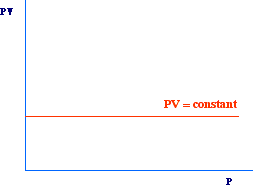
Suppose to have a gas at pressure P1 and volume V1, if we change the pressure, at constant temperature, from the value P1 to the value P2 we will have a change in volume from V1 to V2 and the following equation must hold P1V1 = P2V2 = const According to this equation, another simple way to obtain a straight line,  is to plot PV versus P (or versus V). In this case we will obtain a straight line with slope zero, i.e., parallel to x axis. In fact, for any value of P the PV product should have the same value.

This law states that at constant pressure, the volume of a gas increases linearly with the temperature. In mathematical terms, the laws of Charles and Gay-Lussac is expressed by the following equation:

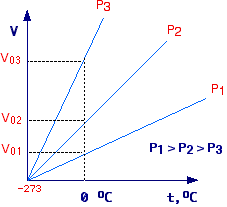
When plotted, this equation  yields a straight line with slope = V_oa.

By plotting experimental values of V versus t, at different constant pressures, a family of straight lines is obtained. For each line, it can be experimentally determined that

slope = V_o / 273.15 hence a = 1/273.15.

Furthermore, each line start from a value of -273.15 °C, in fact for V = 0

V_oat = - V_o from which t = -1/a = -273.15.

Let's consider now a gas a two differents temperature:

t1	t2	By dividing V1 with V2
V1 = Vo(1 + at1)	V2 = Vo(1 + at2)	V1(1 + at1) --- = ----------- V2(1 + at2)

by dividing numerator and denominator with a (= 1/273.15) we obtain:

V₁(273.15 + t₁)
--- = ----------------
V₂(273.15 + t₂)

The term 273.15 + t defines the absolute temperature (Kelvin scale, K), i.e., 

T (absolute temperature) = 273.15 + t

By using T in place of 273.15 + t we get:

V1T1 --- = --- = const V2T2

V --- = const  T

V = (T) (const)

From the last equation we can deduce that the volume of a gas should be zero at 0 K (-273.15 ^oC) and since the volume of a gas can not be negative thus 0 K should be the lowest temperature possible.

 

The ideal gas equation

By combining the Boyle's law and the law of Charles and Gay-Lussac, it can be derived that

T
V = ---- const 
P

This equation states that the volume of a gas increases linearly with the temperature and decreases linearly with the pressure.  

Considering that the volume of a gas depends also on its amount, and taking the moles as unit of measure, we have that const = nR where R is a new constant known as the universal gas constant. The equation above can be then rearranged as follows

 

nRT V = ----- P

PV = nRT

PV ----- = nR = const  T

P1V1P2V2 ------ = ------   T1T2

It is interesting to note that for

T = const	P1V1 = P2V2 , Boyle's law
P = const	V1/T1 = V2/T2; V1/V2 = T1/T2 , Gay-Lussac Law
V = const	P1/T1 = P2/T2; P1/P2 = T1/T2 , Charles Law

The Avogadro law states that different gases at the same values of P, V and T contain the same number of moles. In fact, considering two gases (a and b) at the the same values of P, V and T, we can write:

PV = naRT

PV na = ---- RT

PV = nbRT

PV nb = ---- RT

Since P,V,T are the same and R is a constant, then n_a = n_b. It follows that a given amount of different gases have the same volume when subjected to the same pressure and temperature. The volume of one mole of a gas at 0 ^oC (273.15 K) and 1 atm has been experimentally measured and resulted to be 22.41 liters. This volume is known as the standard molar volume and the condition of temperature and pressure at which it has been determined are known as standard condition and generally abbreviated as STP.

Considering the standard conditions (1 atm and 0°C) and 1 mole of gas, we can easily calculate the value of R :

PV(1 atm) (22.414 liters)(atm)(liters)
R = ----- = ------------------------- = 0.08205 -----------------
nT (1 mole) (273.15 K)(moles) (K)

Remembering that the pressure is given by force/area and area and volume can be expressed in terms of length (L), we have

PVF VF L³FL
R = ----- = ------ = ------ = ----
nTA nTL² nTnT

Since the product of a force with a length is the work which have the same dimensions as energy, we have that the dimension of R, in the SI system, are

energyJoule
-------- = -----------
mole K kg-mole K

It should be evident that the numerical value of R depends on the units used to measure P, V, T. In the appendix you can find a table reporting the values of R when using different units.

Sometimes, when working with a particular gas, it is convenient to include the molecular weight of the gas in R. Remembering that moles = mass/molecular weight, we have

mass
PV = nRT = ------ RT
mw

4 and indicating with R' the ratio of R with mw we have

PV  = mass R' T

where R' is specific for the gas considered.

Dalton's law states that in a mixture of gases each gas exerts the same pressure as it would exerts if it was present alone. Let consider two different gases (1 and 2)

Gas 1 in a vessel with volume V, exerting the pressure p1 RT p1 = n1 --- V

Gas 2 in a vessel with volume V, exerting the pressure p2 RT p2 = n2 ---- V

When the two gases are mixed together in a vessel of volume V, the pressure exerted by gas 1 is still p₁ and the pressure exerted by gas 2 is still p₂. It follows that the total pressure, exerted by the two gas is P_t = p₁ + p₂ and it is given:

RTRT 
P_t = p₁ + p₂ = (n₁ + n₂) ---- = n_t ----
VV

p₁ and p₂ are commonly known as partial pressures.

By dividing the partial pressure of one of the two gases (e.g., gas 1) with the total pressure (equ. above) we get

p1RTVn1 ---- = n1 ---- ------- = ----- PtVRT ntnt

n1 p1 = ------ Pt = xPt nt

where x is the mole fraction (n₁/n_t) of gas 1. In words, the partial pressure exerted by a gas in a mixture is given by the product of its mole fraction with the total pressure (p = xP_t).

According to Avogadro law, at the same condition of temperature and pressure, the volume occupied by any gas depends only on its number of moles thus

p₁/P_t = n₁/n_t = V₁/Vt

these ratios are known as pressure fraction, volume fraction and mole fraction respectively.

The concept above can be applied to any number of ideal gases.

 

Average molecular weight

Consider a mixture of two gas of mass M_t, remembering that moles = mass/molecular weight, we can write

M_t = n₁ Mw₁ + n₂ Mw₂

by dividing with n_t (total moles), we have:

M_t     n₁          n₂
--- = ---- Mw₁ + ---- Mw₂ = x₁Mw₁ + x₂Mw₂
n_t     n_t          n_t

The term M_t/n_t represents the mass of one mole of the gas mixture, i.e., the average molecular weight of the mixture, therefore

Average Mw = x₁Mw₁ + x₂Mw₂

This formula can be applied to mixtures containing any number of gases:

Average Mw = x₁Mw₁ + x₂Mw₂ + ..... x_nMw_n

We have seen before that the term PV has the dimensions of a work (energy), therefore when a gas expand (or is compressed) a work is done (see thermodynamics for more). Let's consider the heating of a gas, in two differents conditions:

1. The gas is heated by maintaining a constant pressure, in this condition the gas expands thus doing a work (PDV). Therefore, at constant pressure, the energy supplied will be part transformed in work and part transformed in kinetic energy thus increasing the temperature of the gas.

2. The gas is heated by maintaining a constant volume, in this condition no work can be accomplished (DV = 0) and all the energy supplied will be transformed into kinetic energy.

The energy needed to raise 1 mole of the gas one degree, is referred to as heat capacity. When this energy is referred to 1 gram (kilogram) of a substance the term specific heat is used. By indicating with C_p and C_v the heat capacity (specific heat) at constant pressure and constant volume respectively we have that

Cp = Cv + PDV

Cp > Cv

Therefore, in constant pressure process,  more energy is to be added to observe the same change of temperature. It can be demonstrated (kinetic theory of gas) that for a monoatomic gas, the variaton of kinetic energy with temperature is given by DE = 3/2 (R DT). From this equation, we have that DE/DT = 3/2 (R), DE/DT is the energy for unit temperature and thus represents the heat capacity. Therefore

At constant volume: C_v = DE/DT = 3/2 (R) = 3/2 (1.987 cal/mol ^oC) = 2.97 cal/mol ^oC.

At constant pressure: C_p = C_v + PDV = C_v + P (V₂-V₁) = R (T₂-T₁) = R DT

Since we are dealing with heat capacity then DT = 1 then C_p = C_v + R = 3/2 (R) + R = 5/2 (R)

From the data above we can calculate the theoretical valuer of C_p/C_v, which is

C_p/C_v = [5/2 (R)] / [3/2 (R)] = 5/3 = 1.67

For monoatomic gas (e.g. He, Ne, Kr), the experimentally determined ratio is very close to 1.67. For diatomic gas (e.g., H₂, N₂, O₂) the ratio Cp/Cv is significantly less than 1.67 (about 1.4).

 

Imperfect gases

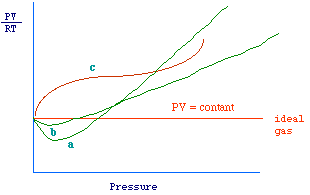
We have seen that for an ideal gas equ 1 and 2 hold. The quantity PV/RT which is 1 when 1 mole is considered, is known as the compressibility factor (generally indicated as z). In fig 1, is reported a qualitative plot of z versus P, it can be observed that For ideal gases a straight line parallel to the axis of pressure is obtained, i.e., z is constant (see 2). For real gases, z is not constant and its value depends on pressure values and on the nature of the gas. Furthermore, at low pressure the value of z approaches the unit. In order to understand such deviations, we should reconsider the assumptions made for the deduction of laws of ideal gases.

1. PV = nRT 2. n = PV/RT = z Fig 1.

The first assumption was that the volume occupied by molecules of an ideal gas is negligible when compared to the volume occupied by the gas. Therefore the volume occupied by the gas is the volume really available to gas molecules for their movements. For a real gas the volume occupied by molecules can not be neglected and thus indicating with b the volume occupied by molecules (known as covolume), the volume really available to molecules should be V - b.

The second assumption was that there is no interactions between molecules. For a real gas the attraction between molecules ("internal pressure" ) leads to a value of pressure which is lesser than that theoretically predictable. Therefore, during the compression of a real gas, the deviation from unit depends on the balance of two contrastant effects: 

Because of covolume, the reduction of the volume should be lesser than that predict by PV = nRT.

Because of internal pressure, the reduction of the volume should be greater than that predict by PV = nRT.

The behavior of real gas can be, with a moderate accuracy, described by van der Waals equation:

(P + a/V²) (V - b) = RT

where a and b are positive constants characteristic for a given gas.

When the pressure is very low V tends to be much larger than b and a/V² tends toward zero and thus the equation reduces to PV = RT.

The inversion can be easily explained by noting that the higher the pressure the lesser the volume and thus the effect of covolume (which is constant) becomes more important. The pressure at which the inversion occurs is known as inversion pressure. As for pressure there exists a temperature of inversion. Above this temperature the effect of covolume is more important than that due to internal pressure. Of course at the inversion pressure and temperature the gas behaves as an ideal gas. Remembering that the product PV is a work, we can deduce that an ideal gas (PV = constant) does not accomplish any work under compression or expansion (thus T = constant).

A real gas, instead, when the pressure is changed can accomplish a positive or a negative work depending on the relative importance of covolume and internal pressure. Let's consider a gas at a temperature above the inversion temperature, i.e. at a temperature for which the effect of covolume is more important than that of internal pressure. From the figure is easy to verify that by increasing the pressure from P₁ to P₂ it will be P₂V₂ - P₁V₁ > 0. Therefore under compression the gas accomplish a work with a consequent decrease of its internal energy and than of its temperature. Of course when the gas is allowed to expand its temperature increases.

For a gas below its inversion temperature (and its inversion pressure) the compression will increase the temperature while an expansion decreases it.

Let's consider the isothermic compression of  carbon dioxide at temperatures less than 31.3 ^oC:

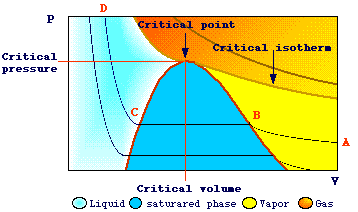At relatively low values of pressure, as the pressure increases, there is a significant decrease of volume (line A-B) .

When the point B is reached, condensation begins and we can observe a decrease in volume at constant pressure (line B-C). At point B the gas is in a so called state of saturation, i.e. it is in equilibrium with its liquid phase.

At point C, where only the liquid state occurs, the increase in pressure results in a small decrease in volume.

If the compression is performed at higher temperatures (less than 31.3^oC), the same behavior will be observed but the change in volume, during the phase change, will be less than that observed before.

When the compression is performed above 31.3^oC (critical isotherm) no liquid will form and there is only a decrease in volume and a corresponding increase in density.

The maximum value of temperature at which condensation can occur is said critical temperature.

The corresponding values of pressure, volume, density are also said critical.

When a liquid is compressed above its critical pressure and then heated to a temperature above its critical temperature a superheated fluid is obtained without boiling. In this process two phases (liquid and gas) are never observed. The fluid obtained in this way is said supercritical fluid.