Thermodynamics

Reversibility and irreversibility

From our daily experiences we know that heat spontaneously flows from a hot body to a cold body, gases spontaneously expand, a liquid in a open container will ultimately evaporate entirely. The reverse is never observed  and all these processes are said irreversible, in that they can not reverse spontaneously, i.e. without external intervention.

On the contrary, a process in which a system can go from the state A to the state B and return back to state A in such a way system and surroundings return exactly to the original condition is said reversible. Although, reversible processes are ideal processes, they are very useful in the study of thermodynamics. 

Let's consider a liquid in equilibrium with its vapor, if we increase the pressure on the system of an infinitesimal amount only few molecules will condense releasing an infinitesimal amount of heat and the process can be turned into an expansion just by decreasing the external pressure of an infinitesimal amount. Virtually system and surrounding are unchanged and thus the process is reversible. On the other hand, if the increase in pressure is finite much vapor will condense and finite amount of heat is transferred to surrounding. The process can not be reversed by an infinitesimal change of pressure or temperature and then it is irreversible. In conclusion, we can define a reversible process the one that can be reversed by an infinitesimal amount of one of its thermodynamic functions (pressure, temperature, etc.). A reversible process is also said a quasi static process.

All natural processes are irreversible for systems are not at equilibrium or for the existence of dissipation of energy due to friction. In the first case, if there is no equilibrium, the system will reach it and the process can not be reversed by an infinitesimal change of its thermodynamic functions. In the second case, in order to reverse the process, in addition of an infinitesimal change in thermodynamic functions we need to furnish the energy dissipated.

Let's consider the work accomplished by a gas during a reversible and an irreversible expansion. During the reversible expansion we have the internal and external pressure will differ of an infinitesimal amount (dP) while during the irreversible process a finite difference of pressure (DP) will exist.

Reversible	Irreversible
Pint = Pex + dP	Pint = Pex + DP
Wrev =PexdV = (Pint - dP)dV Wrev =Pint dV - dPdV	Wirrev =PexdV =(Pint - DP)dV Wirrev = Pint dV - DPdV

The product of two infinitesimal amounts (dPdV) can be neglected while the term DPdV can not be neglected and thus

Reversible	Irreversible
Wrev =Pint dV	Wirrev = Pint dV - DPdV

It is should be evident that evident that W_rev  > W_irrev.

The fact that W_rev > W_irrev can be well illustrated by considering  P-V plots. In A is schematized the reversible process in which the gas expands from V₁ to V₂ by means of infinitesimal decrements of the external pressure.

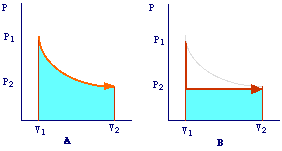
Since P_ex is practically equals to P_int and, for an ideal gas, P_int = nRT/V, we have that:

W_rev = (nRT/V) dV = nRTdV/V = nRT ln V₂/V₁

In other words, the work is represented by the area under the P-V isotherm. In B is reported the representation of the corrispondent irreversible expansion. In this case, the external pressure is first dropped from P₁ to P₂ maintaining the volume constant (thus no work is accomplished) and then the gas is allowed to expand. In this case, the gas will do a work against a constant external pressure (P₂) and then W_irrev = P_extdv = P₂(V₂-V₁) which is represented from the  the area under the curve P-V in plot B. It is evident that W_rev > W_irrev.

In the case of reversible and irreversible compression we still have

W_rev > W_irrev

but since DV is negative the work made on the system is negative thus W_irrev is more negative than W_rev. In other words the work necessary for the irreversible compression of a gas is greater of that required during a reversible compression. Eventually,  from the discussion above it results that work is not a function of state since the work exchanged between system and surroundings depends on the path followed by the system.

Thermodynamics is the discipline which deals with energy transformations and is based on some laws arising from several experimental observations on the behavior of matter. Here, we just gives some qualitative concepts (see later for more).

First law

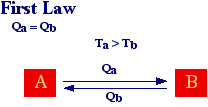
The first law of thermodynamics is the law of conservation of energy and it states that energy can not be destroyed or created but only transformed from one form to another (work, heat). It follows that energy of the universe is constant.

Second law

Let's consider, the exchange of heat between two bodies at different temperatures. The first law tell us that the heat lost by A must matches the heat gained by B and viceversa. Therefore, according to the first law heat can go from A to B or from B to A with the only restriction that energy must be conserved.

However, from our daily experience we know that heat spontaneously flows from an hot body to a cold one and never form a cold body to an hot one (without external intervention). 

The second law essentially states that natural (spontaneous) processes proceed only in a well defined direction. In other words, according to what said before, natural processes are irreversible

Entropy and chaos

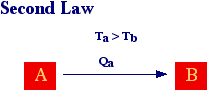It will be shown later that there exists a function of state (entropy, indicated as S) which increases when a spontaneous (irreversible) process takes place. Entropy is defined as

dq
S = ----
T

where dq is the heat exchanged during a reversible process and T the temperature in kelvin at which the exchange occur.

For the case of heat exchange is easily to shown that entropy increases when heat flow from a hot body to a cold one. In fact, the entropy of body A is given by 2 while entropy of body B is given by 3 and since T_A > T_B then S_B > S_A or S_B - S_A > 0.

dq 2. SA = --- TA dq 3. SB = --- TB

Let's consider a substance in the solid, liquid and vapor state. The strength of the interaction between molecules is as follow

Solid > Liquid > Vapor

The consequence is that the freedom of movement of molecules is

Vapor > Liquid > Solid

The vapor state, compared with the liquid and solid state, is the more desordered (chaotic) state in that it is more difficult to predict the position of a molecule.

The solid state, on the contrary, is the less desordered state in that the strong interactions among molecules limit the movements of molecules. For example, in the case of a perfect crystal, each atom occupies a well defined position.

It is not difficult to demonstrate (see later) that

S_vapor > S_Liquid > S_solid

and thus entropy (S) is a measure of the desorder (chaos) of a system, the higher the desorder the higher the entropy. Therefore, according to second law, systems spontaneous evolve from ordered to disordered states.

 

Thermodynamics vs. kinetics

It is worth noting that thermodynamics can tell us if a process can take place but not the rate at which it will occur. For two bodies at differents temperatures, the second law assures that if T_A > T_B heat flows from the body A to body B. The transfer of heat will cease when a state of equilibrium, at which the two bodies has the same temperature, is reached. However, the rate at which the equilibrium is attained will depends on the nature of the material used, i.e., on the ability of the materials to transfer heat. Therefore, it should be evident that for the study of physical phenomena two different approaches are needed: 

1. Given a system, we should know in which direction the system will evolve (in the example of heat, we know that heat spontaneously flows from an hot body to cold one). Thermodynamics deals with this problem. 

2. It is important to know the kinetic of the process, i.e., the rate at which it takes place. Kinetics deals with this problem.