Second Law of thermodynamics
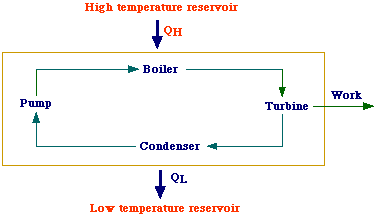An
heat engine is defined as a device which performs a thermodynamic cycle
and produce net positive work by transferring heat from a high temperature body
to a cold one. An example of heat engine is the steam power plant schematized
in the figure. High-pressure superheated steam coming from the generator (boiler)
enters the turbine and expands adiabatically thus generating work. Low-pressure
steam leaves the turbine and enters the condenser where it condense by transferring
heat to cooling water. Next, the pump increases the pressure of the condensate
and allows it to reach the boiler. Therefore, this cycle transfers some heat
from the high temperature resorvoir (HTR) to the low tempetature resorvoir (LTR)
and produces work. Please note that with the term reservoir we indicate an ideal
body to which we can add or subtract heat without changing its temperature.
The steps involved in the process above can be summarized as follows:
1] Reversible isothermal process in which heat is transferred
from HTR to the boiler. This transfer will be reversible if the temperature
of the boiler is infinitesimally lower then HTR. Furthermore, since the temperature
of HTR does not change upon heat transfer (see definition of reservoir above)
also the temperature of the boiler must result unchanged. We can imagine that
water is at is boiling point and the heat transferred from HTR to water is the
latent heat of evaporation of water.
2] Adiabatic reversible expansion of steam in the turbine. As
consequence the steam leaves the turbine at lower pressure and temperature.
3] Reversible isothermal process in which heat is transferred
from fluid to cooling water.
4] Adiabatic reversible compression of steam which leads to an
increase of temperature.
A cycle operating according to the four steps described above (an alternance
of isothermal and adiabatic processes) is known as Carnot cycle. It is
worth noting that since the cycle is reversible (all the processes occuring
in it are reversibles), it can be reversed to obtain a refrigerator (heat pump),
i.e., a device which transfer heat from a cold body to a hot one by using work.
It should be evident that in the heat engine, only part of heat transferred
from HTR to the boiler (QH), for the production of steam, is transformed
in work. The remaining heat is transferred to LTR (QL) during condensation
and thus the work accomplished is given by W = QH - QL.
|
Thermal efficiency is defined as the ratio between the
obtained work (W = QH - QL) and the heat
transferred to the fluid (QH) (see equ. 1). It can be
demonstrated that h is also given by equ. 2,
where T is the absolute temperature, Kelvins. From equs. 1 and 2 it is
easy to deduce equs. 3 and 4.
In the case of a refrigerator the efficiency is defined as QL/W
(coefficient of performance), i.e.,the ratio between the heat transferred
and the work spent to accomplish the transfer (see equ 5).
According to Carnot, given two reservoirs, it is not possible to assemble
a device more efficient than a reversible engine. Furthermore, all the
devices operating on the Carnot cycle using the same reservoir has the
same efficiency.
|
Equ. 1. h = W / QH
=  =
1 - 
Equ. 2. h =  =
1 - 
Equ. 3. =
Equ. 4.  = 
Equ. 5. b = 
|
The second law of thermodynamics can be stated as follows
Kelvin-Planck: It is not possible to assemble a device operating
in a cycle producing only work and exchanging heat with only one reservoir.
In other words, if in the Carnot cycle we eliminate the LTR we should be able
to convert in work all the heat coming from HTR (see
picture) , but this is not possible (100% thermal efficiency). Work can
be accomplished only by transferring heat from HTR to LTR thus implying that
some heat can not be transformed in work.
Clausius: It is not possible to assemble a device operating in cycle
which transfer heat from a cooler body to an hotter body as the only effect.
In other words, by referring to a refrigerator, it is not possible to transfer
heat from a cooler body to a hotter body without an input of work.
By summarizing in both reversible and irreversible processes QH
- QL > 0, thus meaning that only part of the available heat
can be transformed in work. But, in the irreversible process more heat is dissipated
(QLirr > QLrev) and thus less work is obtained (Wrev
> Wirr). It can be demonstrated that any reversible cycle
can be represented by a series of Carnot cycle, therefore the considerations
above hold for any cycle.
Consider
a Carnot cycle that starting from state 1 reaches state 2 through the path A
and returns to 1 trough path B. For a reversible cycle we have that
dQ
/ T = 0 = 
(dQ
/ T )A,1-2 +(dQ
/ T )B,2-1
where the subscripts indicate the path followed (A or B) and the direction
of the process (1 to 2 or 2 to 1). By indicating with S the quotient dQ
/ T we can write
S = SA,1-2 + SB,2-1 = 0
For a cycle going from 1 to 2 through path C and returning to 1 through path
B we have
S = SC,1-2 + SB,2-1 = 0
|
By subtracting these two equations we have:
|
SA,1-2 + SB,2-1-SC,1-2
- SB,2-1 = 0
|
SA,1-2 - SC,1-2 = 0
|
SA,1-2 = SC,1-2
|
This result shows that the value of S is independent from the path followed
and thus it is a property (function of state) of the system. This new function
of state is known as entropy and according to what said above we can write dS
= (dQ / T). In words entropy is the quotient
of heat exchanged by the system with the temperature (in Kelvin) at which the
exchange occurs. It is worth noting that entropy is defined only for a reversible
process and it is an extensive properties.
Let's next analyze the Carnot cycle in terms of entropy considering the working
fluid as our system
|
1. The first process is an isothermal process
where Q is transferred to the fluid and equations a
and b hold. Thus we conclude that the entropy is increased
in going from 1 to 2.
2. The second process is adiabatic and then no entropy
change occurs (isentropic process).
3. The third process is an isothermal process
where Q is transferred from the fluid (our system) to surroundings
and equations c and d hold. Thus we conclude
that the entropy of the system is decreased in going from 3 to 4.
4. The final process is adiabatic and then no entropy change occurs
(isentropic process). Therefore, remembering that S = S1-2
+ S3-4 = 0, we conlude that the increase of entropy in
step 1 perfectly matches the decrease in step 3, i.e. in a reversible
cycle there is no variations of entropy.
|
a. dS = (dQ /
T)
b. S2-S1 =(dQ
/ T ) = Q1-2/T
c. dS = -(dQ
/ T)
d. S4-S3 = -(dQ
/ T ) = - Q3-4/T
|
Entropy
and irreversible processes
|
Consider
that the cycle A-B is reversible and the cycle C-B is irreversible (due to the
fact that the path C is irreversible). By using, for simplicity, finite
variations of heat we can write:
DQ / T = (DQ / T )A,1-2
+ (DQ / T )B,2-1 = 0 (A-B)
DQ / T = (DQ / T )C,1-2
+ (DQ / T )B,2-1 < 0 (C-B).
By subtracting the two equations
(DQ / T )A,1-2 - (DQ
/ T )C,1-2 > 0 and thus (DQ /
T )A,1-2 > (DQ / T )C,1-2
According to our definition of entropy the term (DQ
/ T )A,1-2 represents the change of entropy in going from 1 to 2
through the reversible path A. On the contrary, the term (DQ
/ T )C,1-2 does not represents the variation of entropy in going
from 1 to 2 through the irreversible path C.
| However since entropy is a function of state and does not
depends on the path we can conlude that the variation of entropy in going
from 1 to 2 through the irreversible path C is equal to the change of entropy
in going from 1 to 2 through the reversible path A. Therefore equation e
holds. |
e. (DS)A,1-2
= (DS)C,1-2 > (DQ
/ T )C,1-2
|
| In general, equation i, will hold for
any process. The equal sign in equation i holds for reversible
process while the inequality holds for irreversible processes. In words
when the process is reversible, the entropy matches DQ
/ T while DS > DQ
/ T in a irreversible process. |
i. (DS)1-2
>= (DQ / T )1-2
|
During the discussion above we have considerd only the change of entropy of
the system. Furthermore, we stated that irreversibilty always produces an increase
of entropy and that the entropy of the heat engine can be increased or decreased
by heat transfer. Here we will take in consideration also the change of entropy
of the surroundings. Consider the heat transfer from the surroundings at temperature
T1 to the system at temperature T2:
|
Surroundings (T1)
|
dS1 = -dq/T1
|
entropy is decreased |
|
System (T2)
|
dS2 = dq/T2
|
entropy is increased |
|
Surroundings + System
|
dS = -dq/T1 +
dq/T2
dS = dq (1/T2 -
1/T1)
|
since T2 < T1 thus 1/T2 -
1/T1 > O and dS > 0
for a reversible process (T1 = T2) and thus dS
= 0
|
Therefore we can conclude that only processes for which dSsurroundings
+ dSsystem is positive (at limit zero) can take place. This
is the principle of increase of entropy.
The laws of thermodinamics has been established making no assumption on the
structure of the matter forming a system, in fact a system is described in terms
of macroscopic state functions such as pressure, temperature, volume. However,
we know that the pressure exerted by a gas is due to the collision of molecules
on the walls of a vessel, temperature depends on the average kinetic energy
of molecules, etc. Therefore, in principle, a system could be also described
on microscopic scale by using position and velocity of every atom forming it.
However, the microscopic description of a system, also assuming it is made up
of one mole of a monoatomic gas, is impracticable due the huge number of molecules
presents in it. Moreover, the state of each atom (position and velocity) changes
rapidly and our description would be not valid considering a finite time. The
potency of thermodynamics lies on the use of macroscopic functions (P, V, T..)
of the system which remains constant despite the state of the system changes
at atomic level. In other words, many microscopic states corresponds to the
macroscopic equilibrium state of a system.
Let's consider a vessel, ideally divided in two equal parts, containing 6 molecules
(A to F). Five molecules (N1) are concentrated in the left compartment
and one molecule (N2) is in the right compartment. Since one of the
six molecule can stay in the right compartment and the remaining in the left
one, six possible configurations are possible. The number of configurations
can be calculated as follows
P = N! / (N1!N2!) = 6! / (5!1!) = 720/120 =
6
Consider now, the situation in which N1 = 4 and N2 = 2
P = N!/(N1!N2!) = 6!/(4!2!) = 720/48 = 15
When the gas occupies the whole volume of the vessel, we can expect N1
= 3 and N2 = 3 (for the truth N1 = N2 can be
expected when N is very large as in a real case, here we use 6 molecules to simplify
calculations)
P = N! / (N1!N2!) = 6!/(3!3!) = 720/36 = 20
If we identify P with the number of microstates corresponding to a given macrostate,
we can conclude that during the spontaneous (irreversible) expansion of a gas
the number of microstates increases until to reach a maximum value corresponding
to the equilibrium state. Thus, the behavior of P is the same of entropy (S),
i.e., both increase during an irreversible process. The reasonement above is the
base of the genial intuition of Boltzman which demonstrated that:
S = k log P where k is the Boltzman constant.
The initial state of the example above, having the lower value of P, is an "ordered"
state while the final state (having the maximum possible value of P) is a "desordered"
state. To clarify this point, let's consider what happens when a deck of cards
with a given sequence is shuffled. Before shuffling, the sequence of cards (macroscopic
state) can be described by giving the exact position of each card (microscopic
state) in the sequence. Of course, only one microscopic state (the position of
cards) can describe the initial (ordered) macrostate. After shuffling, cards can
assume any random sequence and many microstates are needed to describe all the
possible sequence of cards in the deck.
){kind=link}