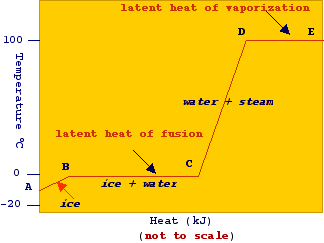
From
these data we can calculate the amount of energy required to accomplish the
heating of 1 kg of ice. According to the picture we have that:
|
Calculation
of sensible and latent heat
|
The sensible heat required to change the temperature of a substance, can be easily calculated as follows:
Q = cp M (T2 - T1)
where:
cp = specific heat, i.e., the amount of heat required to raise 1 °C one kg of substance
M = mass in kg
T1 = initial temperature
T2 = final temperature
Q = heat required for the heating.
Latent heats for most substances have been measured and are tabulated.
In the following table are reported the specific and latent heats involved in the process described in the figure above.
|
Specific heat
|
Water: 4,182 kJ/kg OC |
Ice: 2.05 kJ/kg OC |
|
Latent heat
|
Fusion: 333.2 kJ/kg
|
Vaporization: 2257.06 kJ/kg
|
From
these data we can calculate the amount of energy required to accomplish the
heating of 1 kg of ice. According to the picture we have that:
Line A-B: DT = 0 - (-10) = 10oC ; H = (1) (2.05) (10) = 20.5 kJ
Line B-C: H = 333.2 kJ (Fusion)
Line C-D: DT = 100 - 0 = 100oC ; H = (1) 4.182 (100) = 418.2 kJ
Line D-E : H = 2257.06 kJ (vaporization)
Therefore, the enthalpy required to accomplish the process is
H = 20.5 kJ + 333.2 kJ + 418.2 kJ + 2257.06 kJ = 3028.96 kJ
It is interesting to note that most of the energy supplied serves for the evaporation process (about 74%). For this reason, steam, the vapor state of water, is largely used as source of heat in many engineering fields. In fact, when the vapor is allowed to condense there will be the release of its latent heat of vaporization which can be used for the heating of other substances such as food products. Steam can be produced by using energy from fuel or natural gas (a mixture of hydrocarbon gases that occurs with petroleum deposits, principally methane together with varying quantities of ethane, propane, butane, and other gases).
Eventually, let's note that latent heat as specific heat depends on pressure and temperature. But for the moment we consider them constants in the temperature range considered.
Steam (the vapor state of water) is largely used, in engineering fields, for the heating of other substance. Generally steam is allowed to condensate and the heat liberated used for the heating. Therefore, it is very important to know the thermodynamic properties of steam under different conditions of temperature and pressure.
To illustrate the use of table of steams, here follows a small sample of one
of the tables reported in the appendix. This table reports thermodynamic properties
of steam as function of temperature (first column):
|
|
(kPa) |
(kJ/kg) |
(kJ/kg) |
(kJ/kg) |
(kJ/kg oK) |
(kJ/kg oK) |
(kJ/kg oK) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
The second column reports the vapor pressure of water a the given temperature.
As an example, at 90oC the vapor pressure of water is 70.14 kPa.
Since a liquid boils when the external pressure matches its vapor pressure then
at 90oC and 70.14 kPa of external atmospheric pressure water boils.
By using the terminology introduced above we can say that at 90oC (saturation temperature) the saturation pressure of water is 70.14 kPa.
|
|
(kPa) |
(kJ/kg) |
(kJ/kg) |
(kJ/kg) |
(kJ/kg oK) |
(kJ/kg oK) |
(kJ/kg oK) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Third column reports the enthalpy content (heat content) of liquid water calculated taking as basis 0.01 oC (the triple point of water). In other words, it is assumed that the enthalpy of water at 0.01 oC is zero. Therefore, the values in the third column represent the amount of heat needed for the heating water from 0.01 oC to a given temperature (at the corresponding pressure).
As an example, at 95oC and 84.55 kPa the heat content of water is 397.94 kJ/kg, i.e., we need to supply 397.94 kJ/kg to heat water to the boiling point.
Fourth column reports the latent heat of evaporation, i.e.,the heat needed to obtain the complete transformation of 1 kg of water into vapor.
For example at 95 °C the latent heat of water is 2270.19 kJ/kg.
Fifth column reports the enthalpy content of vapor which is the sum of enthalpy content of liquid (column 3) and latent heat (column 4).
For example, at 95 °C the heat content of steam is
397.94 kJ/kg + 2270.19 kJ/kg = 2268.13 kJ/kg (column five).
Which is the state of water (liquid or vapor) at 95 oC and 70.14
kPa ?
|
|
(kPa) |
(kJ/kg) |
(kJ/kg) |
(kJ/kg) |
(kJ/kg oK) |
(kJ/kg oK) |
(kJ/kg oK) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
From the table it results that at 70.14 kPa, the temperature of saturation is 90oC. Therefore the boiling point of water at 70.14 kPa is 90°C.
Since we are at 95oC, i.e., beyond the boiling point, then water at 95 oC and 70.14 kPa occurs as vapor (steam).
1 kg of steam at 100°C and 1 atm, is used in an heat exchanger to heat a food product. Calculate the amount of heat transderred to the food product when
i) all steam condensates and water exits at 100°C
ii) all steam condensates and water exits at 95°C
In the first case, water exit at 100°C and therefore only the latent heat is transferred to the food. From table, we can see that at 1 atm and 100oC, the latent heat is 2257.04 kJ/kg, therefore the heat transferred is 2257.04 kJ.
In the second case, the heat transferred will be the sum of latent
heat and heat lost by water in going from 100°C to 95°C. From
table it results that
|
|
|
|
|
|
|
|
Therefore the enthalpy transferred to the food product is 2257.04 + 22 = 2279.04 Kj/kg
Let's consider 1 kg of water at 100°C and 101.3 kPa.
If we supply 2257.04 kJ (latent heat), we obtain 1 kg of steam at 100°C and under condensation steam will liberate 2257.04 kJ.
If we supply less than 2257.04 kJ/kg, only part of water will be converted into steam and under condensation steam will liberate less than 2257.04 kJ.
Steam quality is defined as
| Hsupplied
Sq = ----------- 100 Hlatent |
If Hsupplied = Hlatent then Sq
= 100 If Hsupplied < Hlatent then Sq < 100 |
Example. Steam at 100 °C and 101.3 kPa has a quality of 70%. How
much heat it will liberate under condensation ?
| Hsupplied
Sq = ----------- 100 Hlatent |
Hsupplied 70 = ----------- 100 2257.04 |
70
Hsupplied = --------2257.04 = 1580 kJ/kg
100
Therefore, only 1580 kJ/kg will be liberated.