Thermodynamics

A system can be defined as the region of space or amount of matter on which we make controlled experiments. The entities external to the system, which can influence the state of the system, are known as surroundings. Systems are distinguished in

close systems when they can exchange only energy with surrounding;

Open systems when they can exchange both matter and energy with surrounding;

Isolated systems when they can not exchange neither mass and energy.

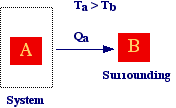Consider two bodies at differents temperature, if the body A (the system) can exchange only heat with body B (the surrounding) then A is a close system. It should be evident that the distinction between system and surrounding is arbitrary and depends on our approach in studying a phenomenon. We could also consider, in other cases, A the surrounding and B the system. Eventually, if body A interact only with body B and viceversa the system formed by body A and B is an isolated system.

Intensive and extensive properties.

The properties of a system can be distinguished into intensive and extensive properties.

Intensive are those properties which are independent from the amount of matter. Examples of intensive properties are temperature and density. If we withdrawn some water from a bottle the temperature and the density of water does not change.

Extensive are those properties which are dependent on the amount of matter. Examples of extensive properties are volume and mass. If we withdrawn some water from a bottle the volume of water in the bottle will reduce (as the mass).

Intensive properties are of greater interest to chemists because they are much more characteristic of the nature of a substance than extensive properties. The division of an extensive property with another extensive property leads to an intensive property. For example, density (m/V) is an intensive properties (does not depend on the amount of substance) while both mass and volume are extensive properties.

 

Equation of state

The volume of a given amount of any material (gas, liquid, solid) depends on temperature and pressure value. An equation of state is the mathematical relation describing the dependence of volume from pressure, temperature and the amount (expressed in moles) of the substance considered. This relation is symbolically expressed as

In words this equation states that the volume of a substance is some function of pressure, temperature and the number of moles of a material. In the case of solids and liquids the equation of state may be very complicated and may differ considerably from one substance to another. On the contrary, the equation of state of all gases is nearly the same. The most simple equation of state for gases is the well known ideal gas equation:

nRT
V = ----- or  PV = nRT (see gases for more).
P

A function of state is a property of a system which depends only on the state of the system and not on the way the state is reached. Typical functions of state are pressure, volume and temperature.

The most important properties of a function of state are

1. Assigning values to few functions of state of a system, all the other functions can be determined. As an example, from equation of state of ideal gases (PV = nRT) it should be evident that once assigned a value to T and V the value of the pressure is univocally determined. Thus a function of state depends only on the values of other functions of state.

2. The change of a function of state depends only from the initial and final state of the system and not on the way the change was accomplished.

3. Furthermore, (see mathematics section), for a function of state it is possible to write an exact differential.

Please note that, in the text, an infinitesimal variation of a function of state is indicated with d (the differential operator) while the symbol d is reserved to other functions.

 

Energy is function of state

Energy of a system.

As already stated, energy is a property of a system which can not be visualized but experiences indicate that energy transfer corresponds to heat transfer and work transfer. In other words, the energy of a system can be changed by heat and work. The energy of a system can be distinguished in

External energy which is the energy of a system associated with its position (potential, E_P) and velocity (kinetic, E_K)

Internal energy (U) which is the energy associated to with atoms and molecules forming the system.

Therefore, the energy of system is given by

E = U + E_P + E_K

Generally, we are interested to the variation of the energy of a system rather than the absolute energy of a system. The total change of the energy of a system in going from one state to another can be written as

DE = DU + DE_P+ DE_K.

Let's imagine an experiment in which some energy is added to a system in such a way it passes from the state A (lower energy) to the state B (higher energy) and let's indicate the variation of energy of the system with E_B - E_A. Now, consider another experiment in which the system returns to the state A by delivering energy, the variation of energy of the system is indicated now with E_A - E_B. There are two possibilities regarding the absolute variations of energy in the two processes, i.e.,

1. ABS(E_B - E_A) <> ABS(E_A - E_B)

2. ABS(E_B - E_A ) = ABS(E_A - E_B)

If equ 1 holds, in going from A to B and then back from B to A we could destroy or create energy. The creation of energy is very attractive, but all the numerous attempts to achieve it have failed and it is. generally accepted that energy can not be created or destroyed. Therefore, equ 2 expresses the right assumption.

In words, when we go back to state A we should recover the same amount of energy spent to go from A to B and thus the energy is conserved. Furthermore since the variation of energy depends only on the initial and final state of the system, energy is a function of state.

The most simple form of work that a system can exchange with surroundings is that associated with variations of pressure and volume. Let's consider a gas which expands against an external constant force (see fig.). When the piston moves from the position r₂ to position r₁, work is given by

W = (fex) (r1 - r2)

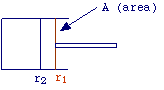
Multiplying and dividing with area, we have:

f_{ex (r1 - r2) (A)}
W = ----------------
(A)

remembering that f/A is a pressure and that the product of area for distance is a volume, equation above reduces to

W = P_ex (V₁ - V₂) = P_exDV

It should be evident that when a gas expands it makes work at the expense of its internal energy, i.e., its internal energy decreases. Conversely, when we compress a gas, the work we make increases the internal energy of the gas.

Consider now two different states for a gas (P₁V₁ and P₂V₂₎ with V₂ > V₁ and of course P₁ > P₂ (see equation of state of an ideal gas). We can change the state of the gas (from P₁V₁ to P₂V₂) in two different ways:

1. The gas is first allowed to expand from V₁ to V₂ against the constant pressure P₁ thus doing a work given by

W = P₁ (V₂ - V₁)

succesively the pressure is lowered to P₂ (keeping V₂ constant). Of course, in this second part of the process, since no displacement occurs W = 0.

2. The pressure on the gas is first lowered to P₂ keeping V₁ constant and thus no work is accomplished. Successively, the change in volume (V₁ to V₂) against the pressure P₂ is allowed. In this case the work is

W = P₂ (V₂ - V₁)

Since P₁ and P₂ are differents, a different amount of work is made in the different paths described. Therefore, work is not a function of state.

 

Heat is not a function of state

Heat is defined as the energy transferred when a difference of temperature exists between system and sorrounding. When a substance is heated, two phenomenona can be generally observed:

1. an increase of temperature (an increase of internal energy)

2. an increase of volume (production of work, W = PDV).

As an example, let's consider the heating of a gas in two different conditions:

Constant pressure process. In this case part of the supplied energy is transformed in work and part produces an increase of temperature (increase of internal energy).

Constant volume process. When no change in volume is allowed, no work can be accomplished and all the energy supplied is used to increase the temperature.

It follows, that the same amount of heat produces a different variation of the temperature (a state function) and thus heat is not a state function. However, if we refer to a constant pressure process heat becomes a state function and is said enthalpy (see later for more). Since most processes take place at constant pressure, the terms enthalpy (H) and heat content are sometimes used synonymously. If a system, under constant pressure, absorbs heat there is an increase of its enthalpy, i.e., a positive change of its enthalpy (DH > 0). Conversely, if the system evolves heat the change of enthalpy is negative (DH < 0).

In the following table are reported the variation of enthalpy (the heat exchanged under constant pressure) for the different phase changes of 1 mole of water at 25°C and 1 atm:

Phase change	DH	Generally indicated as
Evaporation (liquid to vapor)	10519 cal	H2O (l) --> H2O (g) DH = 10519 cal
Condensation (vapor to liquid)	-10519 cal	H2O (g) --> H2O (l) DH = -10519 cal
Sublimation (solid to vapor)	11955 cal	H2O (s) --> H2O (g) DH = 11955 cal
Fusion (solid to liquid)	1436 cal	H2O (s) --> H2O (l) DH = 1436 cal

As can be observed, a solid can be transformed into its vapor by following two different paths:

1. sublimation; 

2. fusion of the solid first and successive evaporation of the liquid. The energy required for sublimation is the sum of the energies required for fusion and evaporation (11955 cal). This proves that enthalpy is a state function.

 

Specific heat

It can be easily experienced that the same amount of heat produces a different increase of temperature in different substances. The amount of heat required to raise the temperature of a fixed amount of a substance by 1 degree celsius is referred to as specific heat. In the SI system specific heat is the amount of energy (Joule, J) needed to raise 1 Kg of material one degree Kelvin. The term heat capacity generally refers to 1 mole of substance.

The amount of heat needed to increase the temperature of a body of mass m from temperature T₁ to T₂ is calculated by

Q = m C (T₂ - T₁)

Since the increase in temperature, of a given substance, depends on the way the heating is accomplished (see above), we need to specify if the specific heat was measured at constant pressure or at constant volume. These two quantities are generally indicated with C_p (constant pressure) and C_v (constant volume).

It is worth noting that specific heat depends on pressure and temperature. However, for the moment, we consider constant pressure processes for which C_p is constant in the range of temperature considered.

Furthermore, let's note that in the formula above we can use indifferently temperatures in kelvin or in celsius. In fact the difference of 1 K corresponds to a difference of 1°C.