By differentiating the equation for free energy (see 1 and 2), we can derive equations giving the dependence of G from pressure and temperature.
| 1. G = H - TS = E + PV - TS | 2. dG = dE + PdV + VdP - TdS + SdT |
Remembering that for a reversible process
dE = Q - PdV = TdS - PdV (first law for a reversible process)
equ 2 can be transformed into
3. dG = TdS - PdV + PdV + VdP - TdS + SdT = VdP - SdT
For a constant temperature process equations 4 and 5 will hold.
| 4. dG = VdP | 5. ( |
In other words, the partial derivative of G with respect to P, at constant temperature, equals V. By integrating and considering an ideal gas (V = nRT/P) we get equations 6 and 7.
| 6. G2 - G1 = DG
= |
7. |
For a constant pressure process equation 3 reduces to 8 and 9.
| 8. dG = SdT | 9. ( |
By combining 1 and 9 we have 10.
| 1. G = H - TS = E + PV - TS | 9. ( |
10. G = H + T ( |
This equation is known as the Gibbs-Helmholtz equation and allows to calculate the change of free energy of a constant temperature process. As an example, consider a chemical reaction which is run at constant temperature, the variation of free energy will be given by 11 and 12.
| 11. DG = (H2
- H1) + T [ |
12. DG = DH
+ T ( |
A function of state depends not only on P, V and T but also on the composition of the system thus in order to define the state of a system we need to specify its compositions (usually the number of moles of each component, ni). The equations derived previously for a variation of G (dG = VdP - SdT) refers to a system with constant composition and tell us that G depends on P and T. More generally, taking as an example a two components system, we should write G = G (P, T, na, nb). Taking the total differential we have:
![]()
The first two terms gives the variation of free energy of the system at constant composition (na and nb are constants) so
dG = VdP - SdT + (![]() G/
G/![]() na)T,P,nb
dna + (
na)T,P,nb
dna + (![]() G/
G/![]() nb)T,P,na
dnb.
nb)T,P,na
dnb.
In this differential equation:
(![]() G/
G/![]() na)T,P,nb
gives the variation of G when the moles of component a
are changed while P,T and the moles of other components are kept constant (b
in the example considered).
na)T,P,nb
gives the variation of G when the moles of component a
are changed while P,T and the moles of other components are kept constant (b
in the example considered).
(![]() G/
G/![]() nb)T,P,na
gives the variation of G when the moles of component b are changed
while P,T and the moles of other components are kept constant (a in the example
considered). These terms are said chemical potentials and are generally indicated
with m. Therefore ma
= (
nb)T,P,na
gives the variation of G when the moles of component b are changed
while P,T and the moles of other components are kept constant (a in the example
considered). These terms are said chemical potentials and are generally indicated
with m. Therefore ma
= (![]() G/
G/![]() na)T,P,nb
and mb = (
na)T,P,nb
and mb = (![]() G/
G/![]() na)T,P,na
are the chemical potential of components a and b respectively. By summarizing,
the chemical potential of a component the system is defined as the change in
free energy of the system when the number of moles of that component
is changed while T, P and the moles of the others components are kept constant.
The total differential of G can be then written as follows:
na)T,P,na
are the chemical potential of components a and b respectively. By summarizing,
the chemical potential of a component the system is defined as the change in
free energy of the system when the number of moles of that component
is changed while T, P and the moles of the others components are kept constant.
The total differential of G can be then written as follows:
dG = VdP - SdT + ma dna + mb dnb
For a system with i components
dG = VdP - SdT + S mi dni
This equation applies to an open system, i.e., the one which can exchange matter with its surroundings. For a close system, since S mi dni = 0 it reduces to dG = VdP - SdT. For a system at constant P and T it reduces to dG = S mi dni. If we consider a closed system consisting of more than one phase, in which mass transfer can occur from one phase to another, we will have
dG = Sami dni + Sbmi dni + ..... = 0
where the superscripts indicate the differents phases the system consists.
The chemical potential defined above is a particular example of what are known as partial molar quantities. The best example to illustrate the concept of partial molar quantity is that concerning the volume of a solution. Wen we mix two liquids, a and b, there are two possibilities:
![]() Ideal
case
Ideal
case
The volume of an ideal solution with two components is the sum of the volumes of the two components taken separately (see 1). In other words, the variation of volume upon mixing is given by 2.
| 1. Vsolution = Va + Vb |
2. Vmixing = Vsolution - (Va + Vb) = Va + Vb - Va - Vb = 0 |
By indicating with Vmb and Vma the volume of one mole of component a and one mole of component b respectively, we can express the ideal case in an other useful way as shown in 3.
3. Vsolution = naVma + nbVmb
where na and nb are the moles of a and b respectively.
Assuming that the number of moles of one component is fixed, it is evident that Vsolution is linearly related to the number of moles of the other component. For example, if na is constant each time we add a mole of b we have an increase of volume corresponding to Vmb.
![]() Real
case
Real
case
The volume of a real solution is not the sum of the volumes of the two components taken separately (see 4 and 5).
| 4. Vsolution <> Va + Vb |
5. Vmixing <> 0 |
As an example if we mix, at 25oC, 100 ml of ethanol with 100 ml of water we get about 190 (not 200) ml of solution (this is due to the existence of complex interactions between molecules).
More important is the fact that Vmixing depends on the composition of the system. This means, for example, that each time we add a mole of B to the solution we will have a different variation of volume. Therefore, the variation of volume should be expressed as a partial derivative (see 6 and 7).
| 6. ( |
7. ( |
Va and Vb are known as the molar partial volume of a and b repectively and they indicate the rate at which the volume of the solution increases when we add a mole of a or b to a given solution. Henceforth, an underlined letter, such as V, will indicate a molar partial quantity.
For an infinitesimal change of moles of a and b, the infinitesimal variation of the volume of the solution is given by 8.
8. dv = (
V /
nb)a dna + (
V /
na)b dnb = Va dna + Vb dnb
Considering a solution with constant composition (thus Va and Vb are constant) we get V = Va na + Vb nb and it can be demonstrated that dVa = -nb/na(dVb). This equation is known as the Gibbs-Duhem equation and allows to calculate the variation of the partial molar volume of a component when the dependence from the concentration of the partial molar volume of the other component is known. We have briefly illustrated the concept of partial molar quantity by using volume as an example but all concepts and equations developped apply to any other extensive thermodynamic function (entropy, enthalpy, etc.). Furthermore all the thermodynamics relations existing between thermodynamics functions can be applied to partial molar quantities. For example we have seen that
(G/
P)T = V
if we consider the partial derivative of the partial molar free energy (i.e.
the chemical potential) with respect to P, we have (![]() G/
G/![]() P)T
= (
P)T
= (![]() m/
m/![]() P)T
= V
P)T
= V
We have seen before that a liquid maintained at constant temperature reaches an equilibrium with its vapor at which the pressure exerted by vapor is constant (known as "vapor pressure") and the evaporation rate match exactly the condensation rate. At the equilibrium, DG = 0 and Gliquid = Gvapor. Since there is no variation of the number of moles of our system (liquid + vapor), i.e., we are dealing with a close system, the equation deduced above:
dGa = VdP - SdT + (RT)[(nb/na)/(nt)] dna + (-RT)/(nt) dnb
reduces to
|
|
|
The meaning of equations 1 and 2 is that, in order that the system be at the equilibrium, at any variation of Gliquid must correspond the same variation of Gvapor. From equ. 2 it is evident that, for a constant temperature process, the only way to change G is a variation of pressure and this variation will be the same for the liquid and the vapor, i.e.,
dGv = VvdP = dGl = VldP
and assuming an ideal behavior for the vapor we have that V = nRT/P and thus
dGv = (nRT/P)dp = dGl = (nRT/P)dp
By integrating the equation above and taking as one limit the vapor pressure of the pure liquid (Po):
DG = nRT ln P/Po
where P is the actual vapor pressure of the liquid. The term P/Po is known as activity and thus:
DG = nRT ln aw
If P = Po , aw = Po/Po = 1, and DG = 0, i.e., we are in presence of pure liquid in equilibrium with its vapor.
It should be realised that in the formula DG = nRT ln P/Po, P is the pressure exerted by vapor on its liquid and that such pressure can be modified by external factors. If we increase the pressure, on the pure liquid, we have P/Po > 1 and DG > 0 thus vapor must condensate to have DG = 0. Conversely, if a decrease of pressure occurs more liquid must evaporate to have DG = 0. Thus, activity of a liquid can be modified by modifying the pressure exerted on it.
Here we got a very important result: the free energy of a component a mixture can be calculated by measuring its vapor pressure. The advantage of this procedure lies on the fact that a vapor follows the ideal gas law better than a liquid.
When a solute is added to the liquid the process of dissolution should involve a diminution of G and as consequence it should be P < Po (to obtain DG < 0). Previously we have shown that for an ideal solution the variation of free energy of a component is also given by
DG = nRT ln x (where ??????????)
where x is the mole fraction of the component considered. Therefore, it should be
|
|
|
|
This last equation represents the Raoult's law which states that the vapor pressure exerted by a liquid depends on its mole fraction. In other words the addition of a solute to a solvent lowers its mole fraction and as consequence its vapor pressure (vapor pressure lowering). The variation of vapor pressure can be written as follows:
DP = P0 - P = P0 - P0 x = P0 (1 - x)
for a solution having only two components 1 - x = xs which is the mole fraction of solute, then
DP = P0xs
i.e., the vapor pressure lowering is directly proportional to the mole fraction of solute. It should be noted that the vapor pressure lowering, depends only on the concentration of solutes but not on their nature. Properties of ideal solutions that depends only on solute concentration and not on the nature of the solute are said colligative properties. An ideal solution is often defined as one which obey the Raoult's law, however an accurate definition of ideal solution is the one given at beginning.
A more accurate procedure to deduce the Raoult's law is to calculate the variation of G when a solute is added to a solvent a T, P, and na (moles of solvents) are constant, we have shown that in such a situation:
dGa = (-RT)/(nt) dnb = (RT/P)dp
dGa = (-dnb)/(nt) = dp/P
Now this equation can be integrated, taking as initial pressure the vapor pressure of the pure liquid (Po). The integration of the term (-dnb)/(nt), assuming that nt is constant (for diluted solutions) lead to -nb/nt. Analogously, if we consider constant the vapor pressure of the pure liquid (this assumption holds for diluted solutions) the integration of dp/Po leads to (P-Po)/Po, thus
(P-Po)/Po = -nb/nt = - xb
by multiplyng with -1 and rerranging
(Po- P) = xbPo
alternatively
Po- xbPo = P
Po(1- xb) = Poxa = P
In real solutions interactions between solute and solvent exists and this can be deduced from the fact that upon mixing we observe absorption or evolution of heat. A common example of nonideal solution evolving heat is one formed by chloroform and acetone.
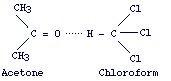 This
is due to the formation of hydrogen bonds which stabilize the two molecules.
Hydrogen bonds do not occur in the pure molecules and thus the attractive forces
between the components of the solution are stronger than those between the molecules
of the same kind. It follows that in solutions evolving heat the vapor pressure
of each component results to be lower than that predicted by Raoult's law (negative
deviation from Raoult's law). On the contrary, for solution that absorbs heat,
a positive deviation from Raoult's law will be observed. Examples of such solutions
are those resulting by mixing polar compounds with nonpolar compounds.
This
is due to the formation of hydrogen bonds which stabilize the two molecules.
Hydrogen bonds do not occur in the pure molecules and thus the attractive forces
between the components of the solution are stronger than those between the molecules
of the same kind. It follows that in solutions evolving heat the vapor pressure
of each component results to be lower than that predicted by Raoult's law (negative
deviation from Raoult's law). On the contrary, for solution that absorbs heat,
a positive deviation from Raoult's law will be observed. Examples of such solutions
are those resulting by mixing polar compounds with nonpolar compounds.
From Raoult's law we know that
x = activity = P/Po
i.e., the activity (P/Po) of a component of a solution where is equal to is mole fraction (x) its concentration.
In real cases we have that x <> P/Po. If we compare the real vapor pressure of the component wih that predicted by Raoult's law we can introduce in the equation above a factor (g, coefficient of activity) in such a way
| gx = a | g = a/x |
The importance of the coefficient of activity should be not undervaluated. We derived (and we will derive), applying the state function G to ideal solutions, a number of very simple but useful equations. Withouth this exemplification, we can expect a more involved thermodynamic analysis of solutions and therefore more complicated equations describing their behavior. By introducing the activity coefficient we can still use the simple equations derived for ideal solutions, provided that activity is used in place of the concentration of components. Finally two important considerations should be made: i) the solvent (i.e., the component which is in excess) has only a slight deviation from the Raoult's law. Thus, with a good approximation, the solvent in diluted real solutions obeys Raoult's law. ii) In normal laboratory practice with chemical equilbria the difference between activity and concentration can be neglected.
Clausius - Clapeyron equation. Let's return to the differentiated form of G obtained previously:
dG = VdP - SdT
and consider again a liquid in equilibrium with its vapor at constant pressure and temperature, or more general a system with one component distributed in two phases (e.g., water-ice, water-steam, etc.). The system will be at the equilibrium when the two phases has the same free energy, indicating with a and b the two phases:
VbdP - SbdT = VadP - SadT
VbdP - VadP = SbdT - SadT
dP (Vb - Va) = dT (Sb - Sa)
dP/dt = (Sb - Sa)/(Vb - Va) = DS/DV
The variation of entropy is equal to latent heat (l) of phase change divided with the temperature at to which the transformation take place and thus:
dP/dt = l/TDV = l/T(Vf-Vi)
this equation is known as the equation of Clausius-Clapeyron and describes the temperature dependence of vapor pressure.
Osmotic equilibrium. Osmosis is a phenomenon occuring when two solutions having different concentrations are separated by a semipermeable membrane. A semipermeable membrane is one that is permeable to the solvent (water), but not to the solute. Actually, a true semipermeable membrane does not exist but there are many membranes (e.g., some animal proteinic membranes) that allows only small molecules to pass through. Let's consider a system, such as the one below, in which pure water (W) and a solution (S, e.g., water and sugar) are separated by a semipermeable membrane. Only water can pass the membrane.
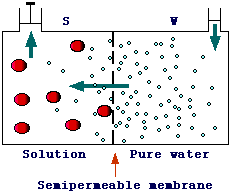 In this system,
a net flow of water from section W to section S can be observed (as indicated
by the increase of water level in S and the decrease in W). This
difference in water level will produce a difference in pression (pS >
pW) opposing the water diffusion from W to S. When this
pression counters exactly the diffusion process an equilibrium is reached and
no net flow of water is observed. The pression at equilibrium is known as osmotic
pressure (p). We have seen previously that the addition
of a solute to a solvent leads to a decrease of the activity of the solvent,
thus the free energy of pure water (W) is greater than G of water in S. In order
to reach a thermodynamic equilibria water must flow from W to S. Let's find
now an expression to calculate the osmotic pressure, i.e. the pressure to exactly
counter the flow of water.
In this system,
a net flow of water from section W to section S can be observed (as indicated
by the increase of water level in S and the decrease in W). This
difference in water level will produce a difference in pression (pS >
pW) opposing the water diffusion from W to S. When this
pression counters exactly the diffusion process an equilibrium is reached and
no net flow of water is observed. The pression at equilibrium is known as osmotic
pressure (p). We have seen previously that the addition
of a solute to a solvent leads to a decrease of the activity of the solvent,
thus the free energy of pure water (W) is greater than G of water in S. In order
to reach a thermodynamic equilibria water must flow from W to S. Let's find
now an expression to calculate the osmotic pressure, i.e. the pressure to exactly
counter the flow of water.
The variation of free energy of this process, for one mole of solution, should be
Gsolution - Gpure water = RT ln P/Po - RT ln (1) = RT ln P/Po
dGsolution = RT ln P/Po = RT ln a = Vsolutiondp
thus in order to counter the process, we must increase the activity of water in the solution in such a way DG = O, i.e. of an amount corresponding to - RT ln P/Po.
Remembering that dG = VsolutiondP, we can increase the activity of water by increasing the pressure. And considering that water is reasonably incompressible, the variation finite of G is
DGsolution = VDP = = -RT ln P/Po= -RT ln xa
where DP is the osmotic pressure of the solution
and xa its mole fraction. And indicating DP
with p :
|
|
|
Which gives the value of the osmotic pressure in function of the activity of
the solvent. Considering that the variation of free energy is due to the adddition
of the solute to the solvent and we shown previously that dGsolution
= (-RT/nt) dnb the equation above can be transformed to give the
pressure osmotic as function of the concentration of the solute. Considering
that in a diluted solution the total number of moles (na + nb)
can be considered constant (na >> nb) we have
|
|
|
For na moles of solvent
pV = naRT xb= naRT nb/(nt)
since na and nt can be considered equals and indicating
with M the molarity of the solution:
|
|
|
Remembering that moles = grams/molecular weight it results that the smaller the molecular weight the higher the osmotic pressure.
Standard free energy of formation (DGfo) is defined as the change of free energy occuring when 1 mole of a compound (in its standard state, i.e., at 298 oK and 1 atm) is formed by its elements in their standard states. Since the standard free energy are tabulated the free energy of substance is more convenient expressed as
G = Go + RT ln (X)
where Go is the free energy of the component with unitary concentration and (X) represents the activity (concentration) of the component.
for n moles
G = nGo + nRT ln (X)
Equilibrium constant. Let's consider a generic reaction
aA + bB = cC + dD
the variation in free energy for the reaction should be the difference of the free energy of products with the free energy of reactants:
DG = Gproducts - Greactants = (cGc + dGd) - (aGa + bGb)
Since the free energy of each component the reactions can be expressed in term of standard free energy, it should be Gproducts = Gop + RT [ln (D)d + ln (C)c]. By rearranging we have:
| 1.
|
2.
|
| 3.
|
4.
|
Gproducts = Gop + RT [ln (D)d + ln (C)c]
where Gop stands for the free energy of products in their standard state.
Analogously
Greactants = Gor + RT [ln (A)a + ln (B)b]
Therefore,
DG = (Gop - Gor)
+ RT [ln (D)d + ln (C)c] - RT [ln (A)a + ln
(B)b]
DG = DGo +
RT ln [(D )c (C)d / (A)a (B)b]
the term DGo is known as the standard free energy of the reaction, i.e., the variation of free energy when all components are at 25oC and have unit activity.
For a system at equilibrium:
DG = 0
DGo + RT ln [(D )c (C)d
/ (A)a (B)b] = 0
since R is a constant and our discussion was limited to isothermic process (T = constant) also the term in square brackets must be a constant. This term is known as the equilibrium constant of the reaction and generally indicated as K:
K = [C]c [D]d / [A]a [B]b
Here, square brackets are generally used to indicate the concentrations at the equilibrium. The numerator of K is the product of the concentration of products, each raised to a a pover equal to its stochiometric coefficients. The denominator of K is the product of the concentration of reactants, each raised to a a pover equal to its stochiometric coefficients. The ratio of this two terms is constant at temperature constant.
We know that for a chemical reaction at equilibrium:
|
|
|
|
|
From the last equation we can see that for DGo < 0 the exponent is positive and thus K > 1, i.e., the products are in larger amount than reactants. Furthermore, the more negative DGo the larger K. The converse will be true when DGo > 0, i.e., K will be less than unity, i.e., the reactants are in larger amount than products. It follows that DGo > 0 does not mean that no products are formed from reactants in their standard states. Furthermore, it is worth nothing that the variation of free energy of a reaction depends on two terms:
DG = DGo + RT ln [(C )c (D)d / (A)a (B)b]
and a reaction having DGo > 0 can proceed spontaneously if the second term in the above equation is negative enough to yield DG < 0. Please note that in the rare case in which DGo = 0, the equilibrium constant will be 1. The exponent of the equation K = 10-DGo / 2.3 RT, remembering that DGo = DHo - TDSo,becomes -(DHo - TDSo)/2.3RT = -(DHo/2.3RT - DSo/ 2.3R) thus
K = 10-(DHo/2.3RT - DSo/ 2.3R)
We have previously remarked that an equilibrium state is a compromise between the tendency of systems to reach a state of minimum energy and the tendency of systems to reach a state of maximum entropy (disorder). The formula above is the quantitatively expression of this general principle. For example, a reaction can proceed to the right also with a decrease of entropy (DS<0) , provided that the variation of H is negative enough to give K>1. Reactions, for which the equilibrium state is characterised by a measurable amount of reactants, are said reversible reactions. This reversibility is the consequence of the existence of the two opposite driving force cited above.
We have already, qualitatively, described LeChatelier's principle, now we will illustrate the thermodynamic basis of this principle. Let's consider again the variation of G for the generic reaction:
aA + bB = cC + dD
for which
DG = DGo + RT ln [(C )c (D)d / (A)a (B)b]
If the system is at the equilibrium DG = 0 and
K = [C]c [D]d / [A]a [B]b
If an external factor produces a variation of the concentration of reactants and/or products the system will not be at the equilibrium (DG <> 0) for term [(C )c (D)d / (A)a (B)b] is changed. Let's examine the different cases:
[(C )c (D)d / (A)a (B)b]> K
the system is not at equilibrium because products are in excess of their equilibrium values and a net conversion of reactants into products will occur.
In the case that
[C]c [D]d / [A]a [B]b < K
the system is not at equilibrium because reactants are in excess of their equilibrium values and a net conversion of product into reactants will occur.
Common ion effect. Let consider a solution of acetic acid, in this solution there is the following equilibrium:
CH3COOH ![]() CH3COO-
+ H+, Ka = [CH3COO-]
[H+] / [CH3COOH]
CH3COO-
+ H+, Ka = [CH3COO-]
[H+] / [CH3COOH]
If we add to the solution a source of H+ (e.g. HCl ) there will be an increase of [H+] which should lead to an increase of Ka. But, in order to maintain constant Ka (i.e., to minimize the effect of disturbance) there will be a decrease of acetic acid dissociation. This is the so called "common ion effect" of LeChatelier's principle.
Changes in volume. A variation of concentration can be also be obtained by changing the volume of the reaction system (variation of pressure, dilution, etc.). Of course, the same variation of concentration for all the components of the system will be obtained, however for a reaction such as
2NO2
N2O4 ; K = [N2O4] / [NO2]2
where the concentration of NO2 is raised to power 2 a decrease of concentration, for example, will increase the denominator more than numerator and thus
[N2O4] / [NO2]2 < K
In this case the reaction will move towards the formation of N2O4 to mantain the value of K. For reactions such as 2A = 2B, K = [B]2 / [A]2, a change in volume (concentration) will influence at the same way numerator and denominator with not affect on the equilibrium. The difference between the two example analysed is that the first reaction (2NO2 = N2O4) involves a different number of chemical species on the two sides of the chemical equation but the second does not. In general when a reaction involves a different number of chemical species on the two sides of the chemical equation an increase in concentration will move the equilibrium to the side containing the lesser number of species. Of course, a diminution of concentration (an increase in volume) will move the equilibrium to the side containing the greater number of species.
Reactions between gases. The equilibrium constant for reactions in gaseous phase is more conveniently expressed in terms of partial pressure (generally in atm, at 25oC) of reactants and products. As an example, for the reaction N2O4 = 2NO2 we have
Kp = P2(NO2) / P(N2O4)
The influence of inert gases. An inert gas is one which is presents in a reaction system but which does not take part to the reaction, e.g., nitrogen is a gas inert during the synthesis of methanol (CO + H2 = CH3OH). Since our discussion is limited to constant pressure processes, the addition of a inert gas leads to an increase of the total number of moles and thus to an increase of the volume of system according to the state equation of gas. An increase of volume is equivalent to a decrease of concentration of the species at equilibrium. Thus, as discussed above, for a reaction leading to an increase of the number of moles the addition of an inert gas will favor the reaction (an increase of number of moles to compensate the diminution of concentration). This effect can be well understood if we express the equilibrium constant in term of mole fractions. For a generic reaction
aA + bB = cC + dD, Kp = (Pc)c (Pd)d/ (Pa)a (Pb)b
the partial pressure can be written in terms of mole fraction and total pressure (Dalton's law):
Kp = (xc Pt)c (xdPt)d / (xaPt)a (xbPt)b
Kp = (xcc xdd / xaa xbb) (Pt)c+d-a-b
since the mole fraction is the moles of a component divided by the total number of moles,
Kp = (ncc ndd / naa nbb) (Pt)c+d-a-b/(Nt)c+d-a-b
Indicating with Kn the ratio of the number of moles and with Dn the term c+d-a-b:
Kp = Kn (Pt/Nt)Dn
Now let's consider the three possible cases:
1. Dn = zero (no variation of the number of moles): (Pt/Nt)Dn = 1 and no effect can be observed after the addition of an inert gas.
2. Dn >0 (increase of the number of moles): (Pt/Nt)Dn decreases. In order to mantain the value of Kp the value of Kn should increase i.e., the reaction is favored.
3. Dn <0 : (Pt/Nt)Dn increases. In order to mantain the value of Kp the value of Kn should decrease i.e., the reaction is not favored and the equilibrium will move to the left.
Of course, the reasoning above is valid only at constant pressure (for which Kp is constant). At constant volume the term Pt/nt in the expression above is constant (PV=nRT; V=P/nRT; if V and T are constant, P/n is constant) and when a inert gas is added, no influence on the equilibria are observed. Inert gases can be also used to control the temperature reached by a reaction system. As an example, consider the combustion of carbon which is usually accomplished with air:
C + O2 + 3.7N2 = CO2 + 3.7N2, DH = -94000 cal/mole
If enough air is used, the complete conversion of C in CO2 will liberate -94000 cal for mole of carbon. The heat liberated will produce an increase of the temperature of the reaction system. By admitting more air than the required air the same heat will be liberated but the temperature will result lower since the heat will be distributed on a greater number of molecules.
Previously we have seen that
K = 10-(DHo/2.3RT - DSo/ 2.3R)
by taking natural logarithm we get
ln K = -DHo/RT + DSo/R
and by assuming that DHo and DSo does not change with the temperature we have that ln K is linearly related to 1/T. We have also seen that
DH2 = DH1 + DCp(T1 - T2)
i.e., DH depends on the difference of the specific heat of products and reactants. In our case we can write
DH = DH0+ DCp(298oK- T2)
and if DCp is near 0 then DH= DH0.
Analogously, for entropy
DS = DS0+ [DCp(298oK- T2)]/T
and if DCp is near 0 then DS= DS0.
Now, if the assumption DCp = 0 holds then ln K = -DHo/RT + DSo/R is the equation of a straight line, i.e., a plot of ln K versus 1/T gives a straight line whose slope is -DHo/R.
For exothermic reactions DH is negative and thus the term -DHo/RT will be positive and will decrease as the temperature increase thus leading to a decrease of K. Conversely, for endothermic reaction the term -DHo/RT will be negative and for an increase in temperature it will be less negative thus leading to an increase of K. Furthermore, the value of DH also determine how rapidly the k increase or decrease for a change in temperature, in fact -DHo/RT is the slope of the straight line. Reactions for which DH = 0 are not affected by changes of temperature.
The effects of temperature on chemical equilibria can be also easily predicted by using LeChatelier's principle. If we increase the temperature the stress is represented by the heat we add to the system and in order to minimize this stress the reaction will move in the direction which absorb heat. On the contrary, if temperature is lowered the reaction will move in the direction that evolve heat.
Let's consider now, the values of K at two different temperature T1and T2:
ln K1 = -DHo/RT1 + DSo/R, ln K2 = -DHo/RT2 + DSo/R
from which we get thatln K2/K1 = -DHo/R (1/T2- 1/T1)
by this equation, if DHo and the value of K at one temperature are known, we can calculate the value of K at any temperature. Furthermore, if the values of K at two different temperature are known, we can also calculate DHo.