Kinetics

The laws of thermodynamics allow to establish if a given process (e.g., a chemical reaction), under certain experimental conditions, can take place but not as fast the trasformation will occur.

Kinetics concerns with the rate at which a trasformation occurs.

Here we shall deal with chemical kinetics, i.e. the kinetics of chemical reactions. However, the concepts we give here can apply to other somewhat different processes such as:

microrganisms growth

microrganisms death under thermal stress.

decay of radioactive nuclei.

biochemical processes (protein synthesis and degradation, enzymatic reactions)

Here follows some examples, to illustrate the importance of both thermodynamics and kinetics in determining the behavior of chemical systems. In general, chemical reactions in aqueous solutions are very fast, two examples of such reactions are:

Ag⁺ + I^- = AgI;      Ag⁺ + Cl^- = AgCl

Consider to add Ag⁺ to an equimolar solution of I^- and Cl^- we can observe only the formation of silver iodide. 

This is due to the fact that the equilibrium constant for the formation of silver iodide is much larger than the constant for the formation of silver chloride (see solubility product). 

A different example, is the dehydration of ethyl alcohol by sulfuric acid, two different reactions can take place depending on the temperature and the concentration of the acid:

CH₃CH₂OH + H₂SO₄ --> CH₂=CH₂ + H₂O (at 170 ^oC in presence of concentrated acid)

CH₃CH₂OH + H₂SO₄ --> CH₃CH₂OCH₂CH₃ + H₂O (at 140 ^oC in presence of dilute acid)

At 170^oC ethylene is the main product while at 140^oC the main product is diethyl ether, this difference is not due to changes in equilibrium constants but at the different rates at which the two reactions proceed in the conditions given above.

Consider a generic reaction as A + B = C + D. If we measure, for example, the variation of [A] with time we can calculate the rate at which A and B are transformed into C and D. However, it is worth noting that in the case of reversible reactions C and D reacts to re-form A and B. Therefore, the rate we measure is a net reaction rate, i.e.,

net reaction rate = forward rate - reverse rate (= 0 at the equilibrium)

Here, we limit our discussion to the case in which the concentration of reactants is far from the equilibrium concentrations and thus the transformation of products into reactants can be neglected. The rate measured in this condition is referred to as initial rate of the reaction and it depends only on the concentration and the nature of reactants.

Let's consider the following generic reaction: A + B = C . If we measure the concentration of A, B and C at different times, we can calculate:
 

rate of  disappearance of A	d[A] - -------- dt	[A] decreases with time thus the minus sign is necessary to get a positive velocity.
rate of  disappearance of B	d[B] - -------- dt	[B] decreases with time thus the minus sign is necessary to get a positive velocity.
rate of  appearance of C	d[C]   -------- dt	[C] increases with the time and thus the positive sign holds.

Since 1 mole di A reacts with 1 mole of B to give 1 mole of C, it should be

 
d[A]d[B]d[C]
v = - ------ = - ------- = ---------
dtdtdt

Therefore one of the expressions above can be used to express the velocity of the reaction.

Consider now another example:2A = B + C

Since two moles of A are needed for the formation of B and C, the rate change of [A] is twice the rate change of [B] and [C] and thus
 

d[A]       2d[B]      d[C] v = - -------- = -------- = --------         dt          dt        dt

or

1   d[A]      d[B]      d[C] v = - --- ----- = -------- = --------        2    dt        dt        dt

Now, a question arise, which of the equations above we take to express the reaction rate ? 

As an example the rate of the reaction is - d[A]/dt or - 1/2 d[A]/dt ? 

In general, the derivative of concentration divided by the stoichiometric coefficient is taken to express the rate of the reaction. In general for a reaction such the following:

aA + bB = cC + dD

        1    d[A]        1    d[B]      1    d[C]       1    d[D]
v = - ----- ------ = - ----- ------ = ----- ------ =  ----- ------
        a     dt         b     dt       C     dt        D     dt

and any of the expressions above can be taken to express the reaction rate.

The differential rate law is the equation expressing how the rate of a reaction depends on the concentration of reactants. Generally, the differential rate law can be expressed as the product of the concentration of reactants each raised to a power. Considering the following generic reaction:
 

where k is the rate constant or better specific rate constant, i.e., the rate of the reaction when the concentration of reactants is the unit. The exponents (m and n) can be integers or half-integers. The exponents in the differential rate law determine the order of a reaction. For example considering the equation above: 
 

v = k [A]n[B]m

if n = 1 then the reaction is of the first order with respect to A if m = 2 then the reaction is of the second order with respect to B. the overall order of the reaction is n + m = 3.

It is worth noting that

the order (the values of the exponents) of a reaction must be experimentally determined.

only in particular cases n and m are equals to the stoichiometric coefficients of the reaction considered.

n and m can be zero (zero order kinetic), i.e. the velocity does not depends on concentration, later we will give examples of this kind of reactions.

Let's consider the two following generic reactions:
 

Consider the following reaction:

H₂O₂ + 2Br^- + 2H⁺ = Br₂ + 2H₂0

According to the observations above, since this reaction implies the collision of five species, the rate of formation of Br₂ should be very low. However, the rate of this reaction, as experimentally determined, is very high. This suggests that the formation of Br₂ does not involves the collision of five molecules.

It has been experimental determined that this reaction take places by means of two different steps:

1) H₂O₂ + Br^- + H⁺ = HOBr + H₂0

2) HOBr + Br^- + H⁺ = Br₂ + 2H₂0

Each of the steps above are referred to as an elementary process and the set of elementary processes by which the overall reaction take place represents the reaction mechanism.

The molecularity of a reaction is defined as the number of species involved in an elementary process.  Considering the example above we have that 

It should be pointed out that elementary processes with molecularity greater than three are not known.

Let's consider the following bimolecular elementary process:
 

A + B = C

it involves the direct collision of A and B to produce C and thus, the reaction rate will be proportional to the concentration of the two reactants: v = k [A][B] (second order kinetic)

In general, for elementary processes

molecularity = order of the reaction.

Although, many reactions have very complex reaction mechanisms, their experimental overall rate laws may be very simple. This is due to the fact that the different elementary processes occur at different rates (ranging from very fast to very low rates) and the overall rate is determined by the rate of the slowest step (rate determining step). Let's consider the following general reaction:
 

Now suppose that the formation of 1 mole of D (step 1) takes 5 minutes while the formation of 1 mole of C takes 50 seconds, we can calculate separately the rate of the two steps:
 

V1 = 1 mole/(300) = O.OO333 mole sec-1

V2 = 1 mole/50 = 0.02 mole sec-1

The overall reaction rate should be V_overall = 1 mole/(300 + 50) = O.OO28 mole sec^-1 and thus the overall reaction rate is less than the rate of the lowest step (1). When the time taken by the faster step is negligible with respect to that of the slowest step,  the overall reaction state will be equal to the rate of the slowest step. By summarizing, the rate of a reaction is limited by the slower step (rate-determining step) and it can be no faster than the rate of the slowest step. In the example reported above, since A + B = D is the slower step, we can write v = k [A][B] and thus complex mechanisms can result in a simple rate law. Let's consider a concrete example:
 

2NO2 + F2 = 2NO2F

the experimental rate law for this reaction is v = k[NO2][F2]

By comparing the rate law with the stoichiometry of the reaction we can affirm that the reaction above is not an elementary process (otherwise a third order kinetic should be obtained by experimental data). The proposed mechanism for this reaction is:
 

NO2 + F2 = NO2F + F (slow step) NO2 + F = 2NO2F     (fast step)

since v = k[NO2][F2] than NO2 + F2 = NO2F + F is the rate-determining step.

Therefore, the determination of the experimental rate law allows to establish if the reaction is described by a single process or by a set of elementary process. The determination of chemical species involved in the different steps require a good knowledge of descriptive chemistry and it is beyond the aims of these pages.

 

The principle of microscopic reversibility

The principle of microscopic reversibility (or detailed balancing) states that at the equilibrium each elementary process and its reverse proceed at the same rate. Let's consider a generic reaction (A = B + C) which is an elementary process. Since this is an elementary process, we can write:

V₁ = k₁[A] (rate of decomposition of A)

V_-1 = k_-1[B][C] (rate of association of B and C)

When the equilibrium is reached, k₁[A]_equ = k_-1[B]_equ[C]_equ from which

k₁[B]_equ[C]_{equ
----- = --------------- =} K_equ
k_-1[A]_equ

Therefore the equilibrium constant for an elementary process is given by the ratio between the kinetic constant of the direct reaction with the kinetic constant of the reverse reaction. Let's consider now a more complex example

Overall reaction	Elementary steps
2NO2 + F2 = 2NO2F	1) NO2 + F2 = NO2F + F 2) NO2 + F =  NO2F

By applying the principle of microscopic reversibility to the two elementary processes we have that at equilibrium:
 

k1[NO2] [F2] = k-1[NO2F] [F]

k2[NO2] [F] = k-2[NO2F]

By multiplying the two equations we have that
 

k1[NO2] [F2] k2[NO2] [F] = k-1[NO2F] [F] k-2[NO2F]

k1k2[NO2]2 [F2] = k-1k-2[NO2F]2

Therefore

  k₁k₂         [NO₂F]²
-------- = -------------- = K_equ (overall reaction)
 k_-1k_-2      [NO₂]² [F₂]

First order kinetic.  Let's consider the differential rate law of a first order reaction, e.g., 
 

the reaction rate of this reaction can be determined by measuring the rate of disappearance of A or the rate of appearence of B. Considering the first case, we write
 

d[A] v = - ----- = k[A]        dt

indicating with c the concentration of A

dc - ------ = kc     dt    dc - ---- = kdt     c

by integrating between c_o (concentration at time 0) and c (concentration at time t) we have that
 

kt = - ln (c/co) = - ln c + ln co

ln c = ln co - kt

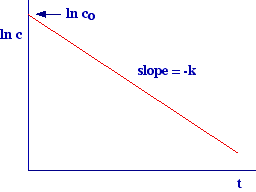The equation obtained above (ln c = ln c_o - kt)  predict that when we plot ln c versus t, we will obtain a straight line thus, if from experimentals data results that ln c decreases linearly with time, we are in presence of a first order kinetic. The plot above also allows the experimental determination of the first order kinetics constant (k).

It is worth noting that decimal logarithms can be used in place of natural logarithms:

2.3 log c = 2.3 log c_o - kt

log c = log c_o - kt/2.3

Starting from ln c = ln c_o - kt, we can deduce another interesting aspect of a first order kintetics. Let's assume that c = c_o/2 and t_1/2 is time required to halve the initial concentration:
 

Therefore, for a first order kinetics the time required to halve the initial concentration does not depend on the initial concentration. The value t_1/2 is referred to as the half-life of the reaction and it is characteristic for the reaction considered.

Eventually, let's note that the equation describing a first order kinetics, can be rearranged to give
 

ln c = ln co - kt

ln c - ln co = - kt

ln c/co  = - kt

c/co  = e- kt

c = c_oe^{- kt}

This equation predicts that for a first order kinetic the concentration of the reagent decreases in an exponential way.

Furthermore, we can note that as t increases c decreases but, from a mathematical point of wiev, c will be never zero. 

In other words, in principle, in a first order reaction (even if it is irreversible), the reagent can not be completely transformed into products.

 

pK from kinetic data

Thiols (R-SH) are weak acids (R-SH = RS^- + H⁺) and they can react with disulfides as follows:

RS^- + R'-S-S- R"  ---> R'-S-S-R + R"-S^- (sulfide-disulfide exchange)

If we relate the rate of the reaction with different initial concentrations of RSH (i.e., without taking in account of dissociation), we can calculate an apparent rate constant:

V =  k_app [RSH]_i [R'-S-S-R'']

where [RSH]_i = [RS^-] + [RSH], i.e., the sum of the equilibrium concentration of the dissociated and undissociated thiol. Therefore,

V =  k_app ([RS^-] + [RSH]) [R'-S-S-R''] (equ. 1).

However, the reaction rate depends on RS^- (which in turn depends on the initial concentration of RSH, from its pKa and from the pH at which the reaction takes place), thus

V = k [RS^-][R'-S-S-R''] (equ. 2)

By dividing equation 1 with the equation 2 we obtain:

[RSH]
k = k_app ( 1 + -------) (equ. 3)
[RS^-]

By rearranging the expression of the dissociation constant of RSH, we have that:

[RS-] [H+] Ka = ------------ [RSH]

[H+]     [RSH] ------ = -------- Ka       [RS-]

By substituting in equ. 3 and by rearranging we get:

[H+] k = kapp ( 1 + -------) Ka

11[H+] ------ = ----- + --------  kappkk Ka

The last equation predicts that a plot of  1/K_app versus [H⁺] will result in a straight line  with intercept  1/k (the true kinetic constant) and slope 1/kK_a. Therefore we can graphically calculate k and K_a.

Reference. A study of the kinetics of the reaction between thiol  compounds and chloroacetamide. Lindley(1960) Biochem. J. 74,557.