Kinetics of microrganism growth and inactivation

Microrganisms. Students should be already familiar with basic microbiology, in this class we just recall some basics concepts. Microganisms (bacteria, yeasts, and molds) may have both harmful and beneficial effects. In fact, microorganism are responsible of spoilage of foods, toxifications, infections. However, they can be also used to accomplish fermentative processes in which carbohydrates are transformed to alcohol or acids. These substances minimize the growth of undesirable organisms and preserve the product. Examples of fermented foods include beer, wine, champagne, bread  (Yeast fermentations)  and yogurt, cheese, fermented sausages (lactic acid fermentations).

The growth of microrganisms depends on several factors such as temperature, pH, water activity, oxygen availability. The regulation of these factor can allow the control of microrganisms growth. 

Influence of temperature

Different microrganisms have different temperature at which they optimally grow and they have been classified as follows:

Psychrophiles	T < 10 °C
Psychrotropic	Tolerate low T. Can grow under refrigeration.
Mesophiles	T = 25-35 °C
Thermophiles	T > 40 °C
Thermotrophics	Tolerate high T. Can grow at 55-60 °C

With few exceptions (e.g., Listeria monocytogenes or Clostridium botulinum) most of pathogen bacteria are mesophilic. Psychrotropic bacteria of the genus Pseudomonas are, generally, the responsibles of spoiling in refrigerated products. The term 'thermal processing' refers to all those operations required to eliminate foodborne ilness, e.g. , heating, cooling.  It have two main objectives: prevention of microrganisms growth (refrigeration, freezing,...) and elimination (or minimization) of microrganisms (pasteurization and sterilization).

Influence of pH

Most of pathogen microorganisms can not grow at pH < 4. Fruit juices are examples of acid foods that prevent pathogens growth.

Influence of water activity

Water activity is given by W_a  = P_w/P_s where P_w is the actual vapor pressure exerted by water and P_s is the vapor pressure exerted by pure water. In order to grow, microorganisms need of appropriate levels of water activity. Generally, with some exceptions, bacteria need a water activity > 0.85 and yeasts and molds > 0.65. The most simple way, to reduce water activity is the addition of solutes (water binding agents such as salts, sugars, polyols, etc.). In fact, from Raoult's law we know that the addition of solutes to water results in vapor pressure lowering (increase of boiling point) and as consequence water activity is reduced. The lowering of water activity can be also accomplished by drying (water activity in dryied foods is about 0.1)

Influence of Oxygen

According to their oxygen requirement, microorganisms are classified as:

Aerobic organisms need oxygen and do not grow in the absence of air. The prevention of their growth is accomplished, in some foods, by sealing the product under vacuum. These foods have to be refrigerated once the packaging is opened.

Anaerobic organisms only grow in absence of oxygen. An example is Clostridium botulinum which produces a lethal toxin. For these organisms sterilization is required if food is packed under vacuum.

Microaerophylics organisms require, for optimal growth, a low level of oxygen but do not grow anaerobically.

 

Kinetics of microrganisms growth

Let's consider a microrganism cell which duplicates after 30 minutes (generation time). Assuming that the new formed cells also duplicate after 30 minutes, we have a system in which the cell population doubles each 30 minutes:

It should be evident that the number of cells at a given time is given by

N = N_o 2^t/x = N_o 2^G

were x is the generation time, t is the elapsed time, N_o is the starting number of cells and G is the number of generations (G = t/x). If we compare, the equation describing the microbial growth (1) with that obtained for a first order chemical reaction (2):

1. N = No 2t/x = No 2G

2. c = coe-kt

we can conclude that microbial growth follows an exponential law (see plot), i.e. a first order kinetics:

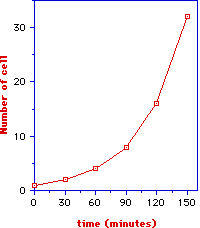
By taking logarithms, equation 1 can be transformed into the equation of a straight line:

Remembering that G is the ratio between time and generation time (x) and indicating 1/x (the inverse of generation time) with k (a constant) we have:

G = t/x = t (1/x)

log2 (N/No) = kt

Lag Time

According to the equation deduced above

log₂ (N/N_o) = kt

the plot of log₂ N versus time will yield a straight line (see plot) with slope k which is equals to 1/x (the inverse of the generation time):

It should be evident that the greater the slope (i.e., the smaller the generation time) the faster the growth.

When cells are placed in a culture medium they do not immediately start to grow in an exponetial manner (plot 3). The time required to reach the linear part of the curve (log growth phase) is known as lag time. The lag time can be evaluated from the plot as shown in figure below:

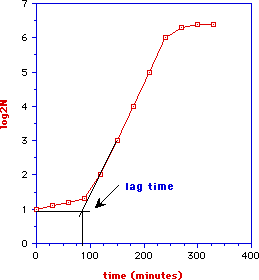
Under ideal growth conditions, microorganisms can double their number in about 30 minutes while in processed foods, due to the stress, organisms surviving commonly exhibit a lag time of 2-4 days. 

In fermented foods, microrganisms are added in an active growth phase thus the lag time is 0 or very small. In order to obtain such microrganisms we need to mantain constant the concentration of substrates.

Another important feature of the plot on the left is that when substrates in the medium is exhausted the growth slows down and then stops. In this situation the lysis of some cells take place thus providing biochemicals for the growth of other cells. Successively, the lysis is generalised and a spore forming process may take place. It is worth noting that it exists an optimal concentration for the growt and that larger concentrations inhibit the growt.

Finally, let's remember that the effect of microorganisms on the safety and quality of foods is dependent on their numbers and that the time required for an organism to reach a specific number depends on three factors: initial population, lag time, generation time.