![]() kt
kt
![]() log c
- log co = - ----
log c
- log co = - ----
![]() 2.3
2.3
co = the initial concentration
c = concentration at time t
t = time
k = kinetic constant.
The decrease of a microbial population, under thermal processing, also follows a first order kinetics and all the relationships deduced for chemical kinetics can be applied. However, in dealing with microrganisms different parameters are used and here we will describe the relationship existing between the parameters used in chemical kinetics and those used in thermal processing of foods.
A first order kinetics is described by the following equations:
|
|
co = the initial concentration c = concentration at time t t = time k = kinetic constant. |
In chemical kinetics, a reaction is generally characterized by its half-life, i.e. the time needed to halve the initial concentration. In other words the time at which c = co/2. By substituting c with co/2 and rearranging, we get an expression for half-life (t1/2):
log (co/2) - log co = - ------ |
log co - log 2 - log co = - ------- |
- log 2 = - -------- |
t1/2 = ------------ = -------- |
From this equation, it should be evident that the time to halve the initial concentration (t1/2) is independent from the initial concentration.
In thermal processing, a different parameter is used to characterize the rate of reduction of a microbial population. This is the decimal reduction time (generally indicated as D) which is defined as the time necessary to destroy 90% of the initial population.
Suppose we have 1000 microrganisms, after a 90% reduction 100 microrganisms will survive and thus the initial population is reduced by a factor of 10 (100 = 1000/10). By indicating with D the time necessary for 90% reduction and substituting c with co/10 in the first order equation, we can obtain an expression for D:
log (co/10) - log co = - ------ |
log co - log 10 - log co = - ------ |
- log 10 = -1 = - ------ |
D = ------ |
It is worth to note that D as t1/2 is independent from the initial concentration.
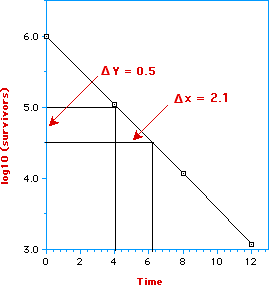
The equation - log (c/co) = kt/2.3 (first order kinetic) represents a straight line with slope = k/2.3:
 Remembering
that D = 2.3/k, i.e., the inverse of the slope, we can easily determine
the decimal reduction time. From the graph we have that
Remembering
that D = 2.3/k, i.e., the inverse of the slope, we can easily determine
the decimal reduction time. From the graph we have that
slope = (Dy/Dx) = 0.5/2.1
D = Dx/Dy = 2.1/0.5 = 4.2 seconds
Normally D values are given with a subscript indicating the temperature at which it refers, as an example D60 indicates the decimal reduction time at 60° C.
As seen above D = Dx/Dy and thus D = Dt / (log co - log c). In other words, D can be defined as the time needed to have a unit variation of log co - log c. A unit variation on a decimal logarithm graph is referred to as a one log cycle, thus D is the time corresponding to one log cycle. As shown above, for a 90% reduction it results that
log co - log 10 - log co = - log 10 = -1.
Therefore one log cycle corresponds to 90% reduction of microbial population. It is worth noting that if we take Dy = 1 (one log cycle) we can directly read, from the graph, the value of D. As an example, in going from 6 to 5 (one log cycle) we can read a value of D of 4.2 seconds.
As for chemical reactions, it is important to know as k (and then D) depends on temperature. The dependence of k from temperature is well described by Arrhenius equation (1 or 2 or 3):
|
1. k = A e-Ea/RT |
2. ln k = ln A - Ea/RT |
3. ln (k/A) = - Ea/RT |
where A is a constant and Ea is the energy of activation.
It should be evident that a plot of ln (k) versus 1/T will be a straight line with a negative slope (- Ea/R), i.e., ln k decreases as temperature decreases.
By taking the reciprocal of the two members of equ 3, we can obtain an equation giving the dependence of ln D from temperature:
1/ln (k/A) = - ln (k/A) = ln (A/k) = ln (A) - ln (k) = - RT/Ea![]()
- ln (k) = - RT/Ea - ln (A)
remembering that k = 2.3/D
-ln (k) = - ln (2.3/D) = ln D - ln 2.3 = - RT/Ea - ln (A)
ln (D) = - RT/Ea - ln (A) + ln 2.3 = - RT/Ea + ln (2.3/A)
 From
the last equation, it results that, a plot of ln (D) versus T will be
a straight line with a negative slope (- R/Ea), i.e., ln D
decreases as temperature increases.
From
the last equation, it results that, a plot of ln (D) versus T will be
a straight line with a negative slope (- R/Ea), i.e., ln D
decreases as temperature increases.
In thermal food processing the dependence of D from temperature is expressed by the thermal resistance constant (z) which is defined as the increases in temperature necessary to have a 90% reduction of D.
As stated before, a 90% reduction, on decimal logarithm scale, corresponds to a unit variation of log (D). Therefore,
z = T2 - T1/ (log DT1 - Log DT2)
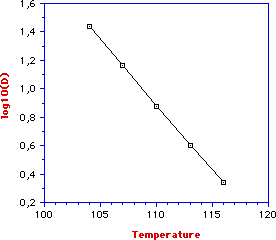
The thermal resistance constant can be easily determined by plotting log (D) versus temperature. For example, from the given graph we can see that by going from 1.4 to 0.4 (one log cycle) the temperature change is 115.2 - 104.2 = 11oC. Therefore, z = 11oC and this means that an increase of 11oC will produce a 90% reduction of D.
The thermal death time, generally indicated as F, is defined as the time required to cause a given reduction in a microbial population and is generally expressed as multiple of D (the time needed for 90% reduction).
For example, consider we want calculate the time needed to have 99.99% reduction in a microbial population. By indicating with F the time needed for 99.99% reduction, the concentration at the time F should be co - O.9999co thus the equation for a first order kinetics is written as follows
From which F = (4)(2.3)/k and since D = (2.3)/k then F = 4D. Therefore, in order to have the 99.99% reduction of a given microbial population, the time of thermal processing should be four times the decimal reduction time.
The value of F can be more easily calculated considering that
![]() c
c![]() -kF
-kF![]() -F
-F
![]() log
---- = log c - log
co = ------ = ------
log
---- = log c - log
co = ------ = ------
![]() co
co![]() 2.3
2.3![]() D
D
From which F = D(log co - log c).
As an example if we have 100 microrganisms and we want only 10 survivors then F = D(log 100 - log 10) = 1D. In fact, in going from 100 to 10 microrganisms we achieve a 90% reduction and thus F is equals to D. Here follows other examples:
| For 99% reduction (1 survivor) | F = D(log 100 - log 1) = 2D |
| For 99.9% reduction (0.1 survivors) | F = D(log 100 - log 0.1) = D[2 -(-1)] = 3D |
| For 99.99% reduction (0.01 survivors) | F = D(log 100 - log 0.1) = D[2 -(-2)] = 4D |
Generally, for the production of shelf-stable foods, the value used is F = 12D where D is the decimal reducing time of Clostridium botulinum.
It is customary, to give F with a subscript indicating the temperature at which it is referred and with a superscript indicating the z value of the microrganism considered. For reference purpose, z is taken = 10oC (18oF) and T = 121 oC (250oF) and this value is indicated as Fo.
We have seen that the time needed for a given % reduction is independent from the initial concentration (first order kinetics). However, it is worth noting that the final absolute amount of microrganisms left in a food product, after thermal processing, depends on the initial population. Let's suppose that our goal is to obtain a food product containing only 10 microrganisms. Starting with an initial population of 100 microrganisms, the time needed for the reduction is D = the time needed for a 90% reduction. If we starts with a population of 1000 units, after the time D the number of microrganisms left will be (0.1)(1000) = 100 thus a longer processing time is needed to reach our goal (10 survivors).
A complete sterilizzation should be attained only after heating for an infinite
time. In fact at each log cycle only 90% of the existing population is destroyed
and a sterile product cannot be obtained with certainity. For food products,
the term commercial sterility is used to indicate that substantially all microorganisms
and spore which, if presents, would be able to grow under defined storage conditions
have been destroyed. However, for a given heat treatement, we can calculate
the probability of surviving of a single microrganisms. Consider a batch of
a food product containing r containers each container having a microbial population
of co, for a first order kinetic is
|
|
|
if t is the total exposure of thermal death time expressed in D units (F)
log (r)(co) - log (r) (c) = F/D
Assume that our purpose is to obtain a batch containing only one microrganism, i.e. only one container retains one microrganism while the remaining containers are microrganisms-free. In these conditions the product rc is the unit and thus
log (rco) - log (1) = log (rco) = F/D
|
|
|
Once fixed F, D and Co, there will be only one value of r satisfying the equation above. This value of r is the number of containers should be processed to have only one microrganism in the entire batch. When more than r containers are analyzed we can not expect the spoilage of only one container. The inverse of r
1/r = co/(10F/D)
is referred to as the spoilage probability, that is the probability to achieve the result.
Example. Assume F113 = 50 minutes, D113 = 4 minutes, co = 104, number of cointainers = 109, using the formula above
r = (10F/D)/co= (1050/4)/104 = 108.5
thus for 108.5 cointainers the spoilage of 1 cointainer can be expected, since the actual number of cointainers is 109 we should expect the spoilage of 109/108.5 = 3.1 cointainers.