-
-NH3+
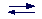 -NH2 + H+
-NH2 + H+
1. Acetylcoline, a neurotransmitter, is quantitatively converted to choline and acetic acid by the enzyme acethylcholinesterase. 15 ml of the neurotransmitter (pH 7.65) are incubated with the enzyme and at the end of the reaction the pH of the solution result to be 6.87. Assuming that there was no buffer in the reaction mixture, calculate the moles of acetylcoline.
pH 7.65 corresponds to 10-7.65 = 2.23 x 10-8 moles/l H+
pH 6.87 corresponds to 10-6.87 = 1.34 moles x 10-7/l H+
Thus the moles/l of H+ formed are
1.34 moles x 10-7 - 2.23 x 10-8= 1.117 x 10-7 mole/l
By inserting this value in the equilibrium constant we can calculate the concentration of acetic acid at equilibrium:
Ka = [H+]2/[ACH][ACH] = [H+]2/ Ka = (1.26 x 10-14)/1.74 * 10-5= 0.72 x 10-9
The initial concentration of ACH formed is then
0.72 x 10-9 + 1.117 x 10-7 = 1.11 x 10-7
The moles of acetic acid formed in 15 ml are:
1.11 x 10-7 x 1000/15 = 1.7 x 10-9
which corresponds to the moles of neurotransmitter originally present.
2. The pka of the amino group of glycine is 9.3. Calculate, for a 0.1 M solution at pH 9, the fraction of glycine having its amino group protonated.
The equilibrium to consider is
-NH3+
-NH2 + H+
for which
pH = pKa - log [-NH3+]/[-NH2]
log [-NH3+]/[-NH2] = pKa-pH = 9.3-9 = 0.3
[-NH3+]/[-NH2] = antilog(.3) = 2
Let z the amount of amino group protonated, thus:
z/(0.1-z) = 2z = 0.2 - 2z
3z = .2
z=.2/3 = 0.066
(0.066 x 100)/.1 = 66%
3. The constant of equilibrium for the reaction N204 (g) = 2NO2 (g) is 0.14 at 25oC. Calculate the fraction of N204 dissociated when the total pressure is 1.5 atm.
Let
|
P1 = partial pressure NO2
|
P2 = partial pressure N204
|
x1 = mole fraction NO2
|
x2 = mole fraction N204
|
The total pressure is then Pt = P1 + P2 = 1.5 atm and the equilibrium constant can be written as follows:
Kp = P12/P2 = P12/(Pt - P1 ) = P12/(1.5 - P1) = 0.14
from which
P12 + 0.14 P1 - 0.21 = 0
This is the well known form of the quadratic equation (see mathematic section). The solution of this equation gives P1 = 0.40 or P1 = -0.53, since the pressure cannot be negative P1 = 0.40. Thus at equilibrium P1 = 0.40 and P2 = 1.5 - 0.40 = 1.1. According to Dalton's law:
P1 = x1Pt and P2 = x2Pt
we can calculate that
x1 = P1/Pt = 0.4/1.5 = 0.27 and of course x2 = 1-0.27 = 0.73
In order to calculate the fraction of N2O4 dissociated, suppose that initially there was 100 moles of N2O4. If d is the number of moles dissociated, at equilibrium we must have:
|
N2O4 = 100 - d
|
NO2 = 2d
|
by inserting these terms in the mole fraction expression we can calculate d:
|
x1 = 2d/(100-d+2d) = 2d/(100+d) = 0.27
|
2d = 27 + 0.27d
|
2d - .27d = 27
|
d = 27/1.73 = 15.6 moles
|
About 15% of N2O4 dissociates, corresponding to the fraction 15/100 = 0.15.
On some books you can find the following formula to quickly solve the above problem:
Kp = 4d2Pt/(1-d2)
Since this formula can be difficult to remember and it is valid only for reactions of the same kind of the one considered above, we preferred to illustrate the solution of the problem by applying the general simple laws of gases.
For the solution of this problem we solved a quadratic equation which is quite simple to handle, however in many technical problems cubic or quartic equation, very tedious to solve, can be encountered. We shall illustrate here an approximate method for the solution of the quadratic equation above which can be easily applied to cubic or more complex equations.
Kp = P12/(1.5 - P1) = 0.14
Let's assume (arbitrarily) that P1 is negligible compared to 1.5 thus
|
P12/1.5 = 0.14
|
P12 = 0.14 x 1.5
|
P1 = 0.45
|
if this value is substituted in the equation of Kp, we have
Kp = 0.452/(1.5 - 0.45) = 0.19
the value obtained for Kp is significantly different from the true value (0.14). However, if we use the value of P1 in the equation of Kp we can improve our result:
|
P12/(1.5 - 0.45) =
0.14
|
P12/1.05 = 0.14
|
P12 = 0.14 x 1.05
|
P1 = .38
|
When this new value for P1 is used to calculate Kp we have
Kp = 0.382/(1.5 - 0.38) = 0.128
This new value of Kp still differs from the true value but less than the value calculated before
Again let's use the new value for P1 to get another approximate value for P1:
|
P12/(1.5 - 0.38) =
0.14
|
P12/1.12 = 0.14
|
P12 = 0.14 x 1.15
|
P1 = 0.395
|
Now we can calculate a new value for Kp
Kp = 0.3952/(1.5 - 0.395) = 0.141
which is practically identical to the true value of Kp thus meaning the the value of P1 is a good approximation of the true value. In fact the value obtained by using the solution of the quadratic equation is 0.40.
By making further iteration we have
|
P1 = 0.41
|
P1 = 0.390
|
P1 = 0.394
|
We can conlude that the method of successive approximations leads at each iteration to values converging to the true value. When two succesive values differ negligibly, the final value is a satisfactory approximation of the the true value.
The method described is arithmetically very simple and can be very useful in those problems were cubic or quartic equation mus be solved (or in the case you do not remember the formula for the solution of a quadratic equation).
5. Consider again problem 4 and calculate the fraction of N204 which dissociates when by increasing the volume of the system of reaction the pressure falls to 1 atm.
First let's try to predict the effect produced by a decrease in pressure (or an increase in volume). Since during the reaction there is a variation of the number of mole the equilibrium should be influenced by a change in pressure. Let' s write the equilibrium constant in terms of mole fraction:
Kp = (x1Pt)2/ x2Pt = x12Pt/ x2 = (x12/ x2)Pt
As can be seen a decrease in pressure must result in an increase of (x12/x2), which can be obtained with an increase of the fraction of N2O4 which dissociates.
In order to calculate the new fraction which dissociates we can express Kp in terms of x1 and solve the quadratic equation (try also the approximate method as made in problem 4):
Kp = (x12 / 1- x1)Pt
from which results x1 = .31 corresponding to d = 0.18 (see problem 4 for details about calculations).
6. Considering again the reaction N204 (g) = 2NO2 (g) calculate the partial pressure of N204 (P2) when the partial pressure at the equilibrium of NO2 (P1) is 0.23 atm.
Kp = (P12 / P2) = 0.14
Kp = (0.052 / P2) = 0.14
P2 = 0.052 / 0.14 = 0.38 atm
7. Solid ammonium hydrosulfide dissociates in ammonia and hydrogen sulfide according to the following equation:
NH4HS = NH3(g) + H2S(g), Kp = 0.11
the value of Kp include the concentration of solid at equilibrium. Calculate the partial pressure of the two gases when some solids NH4HS is added to a flask containing 0.50 atm of ammonia.
Kp = PNH3 PH2S
there are two source of ammonia, the ammonia already present and the ammonia liberated from the dissociation:
PtNH3 = 0.5 + PNH3
According to the stoichiometry of the reaction, PNH3 = PH2S
PtNH3 = 0.5 + PH2SKp = (0.5 + PH2S) PH2S = 0.5PH2S + (PH2S)2
0.5PH2S + (PH2S)2 - Kp = 0
Solving the quadratic equation we obtain PH2S = 0.17 and PNH3
= 0.5 + 0.17 = 0.67 atm.
8. Calculate the solubility of CaF2 (Ksp = 1.7 x 10-10) in a solution of 0.1 M Ca(NO3)2.
CaF2 = Ca++ + 2F-Ksp = [Ca++][F-]2 = 1.7 x 10-5
the total concentration of Ca++ should be:
Ca++nitrate + Ca++fluoride = 0.1 + Ca++fluoride
from the value of Ksp and considering that the dissociation of CaF2 is depressed according to the LeChatelier principle, it can be deduced that the concentration of Ca++ coming from CaF2 is small compared to 0.1 M thus we assume that the total concentration of calcium is 0.1 M
Ksp = [0.1][F-]2 = 1.7 x 10-10[F-]2 = 1.7 x 10-10/ 0.1
[F-]= 1.7 x 10-10/ 0.1 = 4.1 x 10-5
since each mole of CaF2 which dissociates give raise two moles of F-, the solubility of calcium fluoride is
4.1 x 10-5/2 = 2 x 10-5 M
This result justifies our neglect of the Ca++ coming from CaF2.
9. A solution contain 0.1 M Cl- and 0.001 M CrO4--. The Kps for AgCl and Ag2CrO4 are:
KpsAgCl = 2.8 x 10-10
KpsAg2CrO4 = 1.9 x 10-12
If silver nitrate is slowely added to the solution, calculate the amount of Cl- left in solution when Ag2CrO4 starts to precipitate.
From the value of Kps we can calculate the concentration of Ag+
at which Ag2CrO4 starts to precipitate.
KpsAg2CrO4 = [Ag+]2 [CrO4--] = [Ag+]2 0.01 = 1.9 x 10-12[Ag+]2 = 1.9 x 10-12/0.01[Ag+] = 1.4 x 10-5
by inserting this value in the kps of AgCl we can calculate the concentration
of chloride ion at equilibrium with the calculated concentration of Ag+:
KpsAgCl = [Ag+] [Cl-] = 1.4 x 10-5[Cl-] = 2.8 x 10-10
[Cl-] = 2.8 x 10-10/1.4 x 10-5 = 2 x 10-5
The concentration of Cl- is very small compared to the original concentration (0.1M), thus the precipitation can be considered quantitative.
10. Calculate 1) the pH of a solution which is 0.15 M in HCl and 0.05 M in NaOH and 2) the pH of a solution which is 0.05 M in HCl and 0.15 M in NaOH.
This solution can be considered equivalent to a solution 0.1 M (0.15 - 0.05) in HCl thus
pH = -Log (0.1) = 1
In the same way a solution 0.05 M in HCl and 0.15 M in NaOH, can be considered equivalent to a solution 0.1 M in NaOH thus
pOH = -Log (0.1) = 1
pH = 14 - 1 = 13
11. Calculate the pH of a solution 1M in HCl and 1M in NaOH.
In this case the only source of H3O+ is water dissociation thus pH = 7 as in pure water.
Note: The solution above is equivalent to a solution 1M in NaCl, i.e., the salt formed by the strong acid HCl and the strong base NaOH.
12. Calculate the pH of a solution obtained by mixing 500 ml of 0.1 M HCl and 500 ml of 0.05 M ammonia (NH3).
500 ml of 0.1 M HCl contains 0.05 moles of the acid, after mixing the volume is 1 liter thus HCl concentration becomes 0.05 M. Analogously NH3 concentration becomes 0.025 M. The reaction of neutralization can be written as:
NH3+ H+ --> NH4+
This reaction will produce 0.05 - 0.025 = 0.025 moles/liter of NH4+ leaving 0.025 moles/liter of H+. Therefore:
pH = - log 0.025 = 1.6
13. Calculate the pH of one liter of solution prepared by mixing 1.3 moles of acetic acid (pKa 4.75) and 0.6 moles of NaOH.
[CH3COO-] = 0.6 M (the concentration of the base added)
[CH3COOH] = 1.3 - 0.6 = 0.7 M
pH = pKa - Log [CH3COOH]/[CH3COO-] =
4.75 - Log (0.7) + Log (0.6) = 4.68
14. Calculate the pH of one liter of solution containing 0.6 moles of sodium acetate and 0.7 moles of acetic acid.
This problem is perfectly equivalent to the one above. In fact, the dissociation of sodium acetate (strong electrolytes) produce 0.6 moles of acetate. Thus, we will have a solution containing 0.6 moles of acetate and 0.7 moles of acetic acid. In this case the equation used above assumes the following form:
pH = pKa - Log Ca/Cs
where Ca is the concentration of the acid and Cs the concentration of the salt. Thus
pH = 4.75 - Log (0.7) + Log (0.6) = 4.68