

Next: 1.2.1.3 Magnetostatic energy
Up: 1.2.1 First-order Variation of
Previous: 1.2.1.1 Exchange
Contents
As far as anisotropy is concerned, taking the first-order
variation of the energy
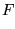 an is equivalent to write the
following equation:
an is equivalent to write the
following equation:
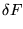 an an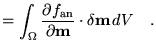 |
(1.59) |
For instance, referring to the case of uniaxial anisotropy and,
therefore, to Eq. (1.43), the latter equation
becomes
Massimiliano d'Aquino
2005-11-26