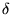 |
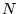 |
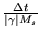 [ps] [ps] |
NR |
LIN |
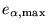 |
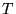 [ns] [ns] |
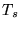 [s] [s] |
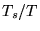 [s/ns] [s/ns] |
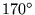 |
1000 |
2.5 |
11/14/17 |
4/5/5 |
 |
5.7700 |
648.05 |
112 |
 |
2500 |
2.5 |
11/14/17 |
6/7/7 |
 |
5.8450 |
1976.47 |
338 |
 |
6400 |
2.5 |
11/14/18 |
11/13/15 |
 |
5.8400 |
5631.23 |
964 |
 |
10000 |
2.5 |
11/14/18 |
17/19/22 |
 |
5.8425 |
12152.74 |
2080 |
 |
1000 |
2.5 |
11/14/17 |
4/5/5 |
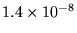 |
5.5800 |
632.34 |
113 |
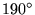 |
2500 |
2.5 |
11/14/18 |
6/7/8 |
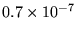 |
6.4100 |
2183.36 |
341 |
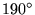 |
6400 |
2.5 |
11/14/18 |
12/13/15 |
 |
6.4100 |
6257.13 |
976 |
 |
10000 |
2.5 |
11/14/18 |
18/20/23 |
 |
6.4100 |
13546.79 |
2113 |
 |
6400 |
1.0 |
9/12/14 |
6/6/7 |
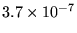 |
5.8420 |
10145.46 |
1737 |
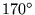 |
6400 |
2.5 |
11/14/18 |
11/13/15 |
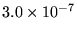 |
5.8400 |
5631.23 |
964 |
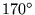 |
6400 |
5.0 |
14/18/25 |
24/26/28 |
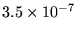 |
5.9400 |
4624.31 |
779 |
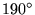 |
6400 |
1.0 |
9/12/14 |
6/6/7 |
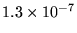 |
6.4150 |
11163.490 |
1740 |
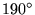 |
6400 |
2.5 |
11/14/18 |
12/13/15 |
 |
6.4100 |
6257.13 |
976 |
 |
6400 |
5.0 |
14/18/27 |
23/26/30 |
 |
7.4950 |
5705.520 |
761 |
|