5 Effetto del ritardo di tempo

• Il ritardo di tempo \(\tau \) si può modellare come un sistema SISO la cui uscita replica l’ingresso ritardandolo di un tempo \(\tau >0\), ovvero con il modello ingresso-uscita \[ y(t) = u(t-\tau ) \Leftrightarrow Y(s) = e^{-s\tau }U(s) \]
• La funzione di anello in presenza di ritardo di tempo si può scrivere nella forma \[ L'(s) = L(s)e^{-s\tau } \]

• Il criterio di Nyquist si applica anche in presenza di ritardo di tempo, in particolare risulta:

  • \(\vert L'(j\omega )\vert = \vert L(j\omega )e^{-j\omega \tau }\vert = \vert L(j\omega )\vert \)
  • \(\arg (L(j\omega )) = \arg (L(j\omega )e^{-j\omega \tau }) = \arg (L(j\omega )- \omega \tau \)

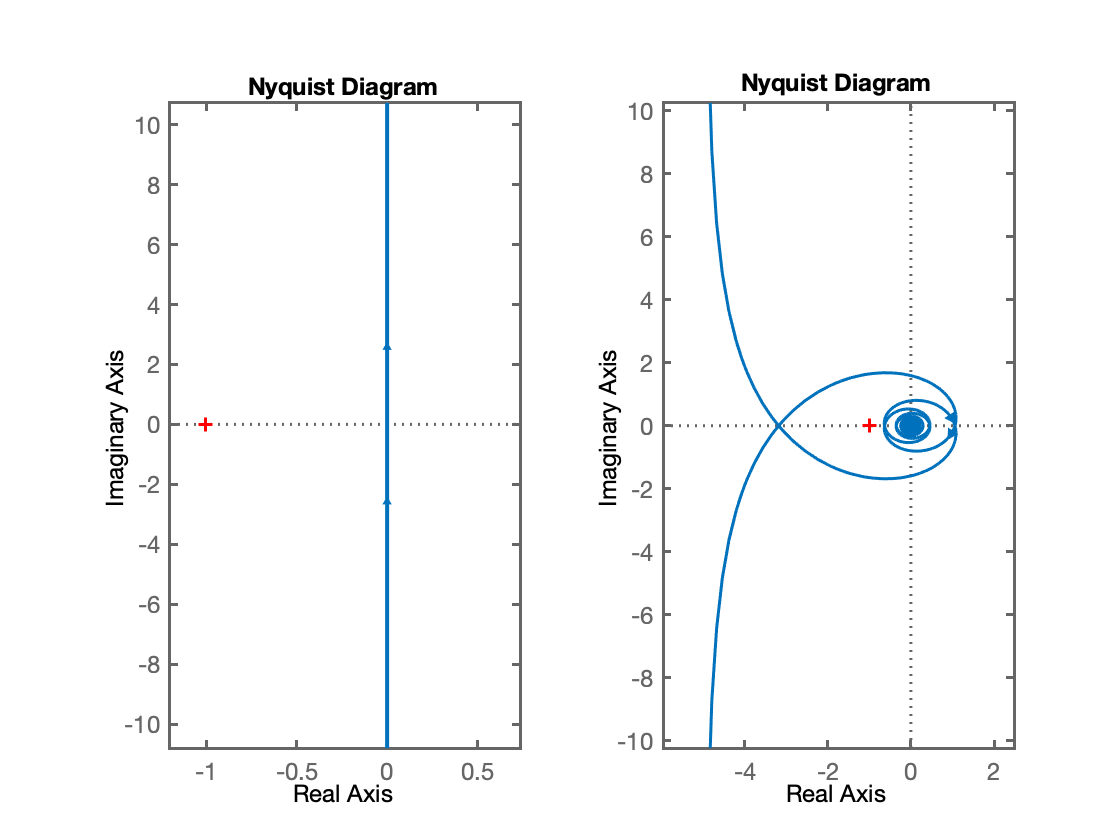
• Il ritardo temporale produce un ritardo di fase che aumenta al crescere della pulsazione ed è chiaramente destabilizzante. Ad esempio, la funzione di anello \[ L'(s) = \frac {5}{s}e^{-s\tau } \] per \(\tau =0\) è intrinsecamente stabile mentre, per qualsiasi \(\tau >0\) è a stabilità regolare, come si evince dai diagrammi di Nyquist di figura