- ... Gibbs1.1
- In Ref. [20] this free
energy is called Landau free energy
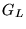 to distinguish
from the Gibbs free energy
to distinguish
from the Gibbs free energy 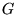 . Here we perform an abuse of
notation.
. Here we perform an abuse of
notation.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
stationary1.2
- It can be shown that metastable equilibria are
minima of the free energy (1.17). In this sense
the minimization of the free energy (1.17)
generalizes the minimization of the Gibbs free energy that holds
in equilibrium thermodynamics.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
equilibrium1.3
- although the whole body is not in
equilibrium, one assumes that each elementary volume is in
equilibrium
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
magnitude1.4
- We will discuss this aspect in
section 1.3.5
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... meanings2.1
- The term shape anisotropy recalls the
fact that magnetostatic field depends on the geometry of the body,
whereas the crystalline anisotropy depends on the lattice
structure of the material.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
components2.2
- The external field is supposed to be
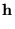 a
a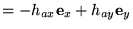 , with
, with 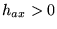 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
values2.3
- We recall that the applied field is expressed here
as
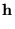 a
a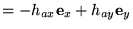 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... (see2.4
- Notice that here the
role of easy axis
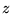 is played by the
is played by the 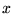 axis.
axis.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
functions2.5
- See Appendix B.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
energy2.6
- We notice that a fixed point is a degenerate
periodic trajectory.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
charges3.1
- Recalling the Coulomb approach to magnetic
materials, which is in term of equivalent volume charges
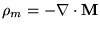 and surface charges
and surface charges
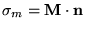 . See Ref. [13] for details.
. See Ref. [13] for details.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... thin-films3.2
- The S-state was obtained by first
saturating the thin-film along the
![$ [1,1,1]$](img1031.gif) direction and then by
switching the external field off.
direction and then by
switching the external field off.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... elliptic3.3
- See Appendix B
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
media3.4
- Since the medium ``sees'' the external field as
applied at 135
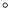 off the easy axis, this can be understood
by looking at the Stoner-Wohlfarth astroid (see
Fig. 3.16) in the direction at 135
off the easy axis, this can be understood
by looking at the Stoner-Wohlfarth astroid (see
Fig. 3.16) in the direction at 135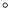 off the
off the
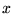 axis, where the critical field is about
axis, where the critical field is about 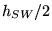 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... field3.5
- This can be
inferred by observing that directions at about 135
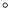 off the
off the
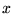 axis intersect the SW astroid at almost the same distance from
the origin. This leads to very close values of critical fields.
axis intersect the SW astroid at almost the same distance from
the origin. This leads to very close values of critical fields.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... dynamics3.6
- We have already seen an example of
switching below SW limit, namely the precessional switching
analyzed in section 2.4.3.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... conservative4.1
- We have seen examples of
this in chapter 2, for uniformly magnetized particles.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.